The shear force on the pins will depend on the angle of the disk and the Force from the maximum allowable torque of the shaft. An angle of 45 degrees is a good approximation

The diameter of these pins must be given to determine the cross sectional area and the resulting shear stresses in the pins.

Therefore the shear stress on the pin is:

This force is acting at an angle to the pin. If we take the

component of this force that is acting normal to the pin, the

maximum shear force can be calculated.

The Force located at this point on the

shaft can be calculated using the equation:

We can picture that on the onset of the seizure the small pin

will remain stationary with the disk and the shaft pin will

try to keep rotating. (Hopefully this will not be the case, but to

determine the maximum shear force, we will assume this).

Therefore, given the distance from the center of the fuel drive

shaft to the point of contact between the disk pin and the shaft

pin, the maximum force acting on the pin can be determined:

This analysis will take into account the forces acting on the pin that holds the shaft disk to the shaft pin. the intent is to determine whether the forces encountered during a seizure will shear the small pin. Again we assume the maximum torque to be:

4.0 Shear Stress Analysis- Part 2 (pivoting pin on disk2 -shaft side)

Therefore it appears that stainless steel would be a suitable material for the pins

And the Tensile yield Strength is:

For Type 301 cold rolled stainless steel:

In this case, this steel would not be suitable for the pins

However the Tensile yield Strength is:

For 1040 hot rolled steel The ultimate tensile strength is :

Depending on the material chosen for the pins, this design may or may not hold up to the required torque levels.

6.0 Conclusion

The above calculations will allow the design team to select a suitable spring which will allow the system to disengage at the required torque level. The analysis above has also allowed the team to select materials for the components which will be suitable for the operating forces involved in the design.

If we compare this value to the above material strength values for steel

and stainless steel it is evident that either of the materials could be used.

However, considering that this is also a very small component and

the amount of error in our approach and calculation is unknown,

it may be a wise decision to use stainless steel to compensate

for any possible error

Therefore the maximum shear stress acting on the pin is:

The minimum cross sectional area of the shaft pin is determined from the diameter:

The resulting force at the distance specified is calculated using the equation:

The maximum torque is obtained from the previous analysis:

In this analysis we will determine if the shaft pin that is

secured into the shaft will shear at the maximum

torque limit. The shaft pin is located a distance from

the center of the shaft which is:

Depending on the material chosen for the pins, this design may or may not hold up to the required torque levels.

For 1040 hot rolled steel The ultimate tensile strength is :

However the Tensile yield Strength is:

In this case, this steel would not be suitable for the pins

For Type 301 cold rolled stainless steel:

And the Tensile yield Strength is:

Therefore it appears that stainless steel can be used for the pins to withstand the shear

stresses involved.

5.0 Shear Stress Analysis- Part 3 (shaft pin connecting disk2 to shaft)

The distance of the force acting on disk one from the pivoting axis of the disk

is found from the equation:

But first the distances d2 and d1 must be calculated

The width of the disks must be specified to find the

distance between the two pivoting axes of the disks. Again from our final design geometry we have:

By analyzing the moment about the pivoting

axis of disk 1 we can solve for this spring force:

:

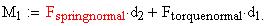
During normal operation this normal force is balanced by

a force from the spring in a direction that directly opposes it.

The normal force acting on the

disk from the spring is determined by:

Senior Design Project 2000/2001

Seizure Recovery System for Fuel System Distributor

Final Design Concept Calculations and Analysis

Sponsored by:

Cummins Engine Company

Team Members:

Michal Brown

Sean Edwards

Keron Miller

Ben Nuttall

Faculty Advisor:

Dr. Farrukh Alvi

Course Instructor:

Dr. Cesar Luongo

1.0 Introduction:

The choice for our final design concept which will be built and tested is concept #4. The basic operating principle behind this concept involves two small disks which are able to pivot. The two disks are placed so that one surface of each disk is in contact with the other. A spring applies pressure to one end of a disk a distance away from the pivoting point. While at an angle the disks allow torque to be transmitted during the case of normal operation. In an overloaded condition, the design of the system allows the spring to be compressed and the disk become perpendicular to the axis of rotation of the shaft. While in this position the shaft is able to spin while the downstream components are seized.

It is desired to calculate some of the forces involved in the design and to choose a suitable spring which will allow the system to disengage at the desired torque level. It is also necessary to perform stress analyses to determine suitable materials for the components. The following calculations will allow the design team to accomplish this.

For the geometry of the current design please refer to the manufacturing drawings. They can be found on the project web page at www.eng.fsu.edu/~nuttall/cummins (page will be later moved to http://www.eng.fsu.edu/~luongo/design/current.ht ml)

2.0 Spring Force Analysis

The desired disengagement torque limit specified by Cummins is given as:

A tangential force will result on the end of the shaft

which will depend on the radial distance between this point

and the axis of rotation of the drive shaft

For a given radius:

The Force located at this point on the

shaft can be calculated using the equation:

The geometry of the design will place a normal force on the second disk as a result of the force from the torque. Based on the angle of the disk this component of the force can be found. The reaction force from the second disc is equal to this force when the system is in equilibrium.

From the geometry of our final design, a maximum angle of the disk is determined and used in the force analysis.

The shear force on the pins will depend on the angle of the disk and the Force from the maximum allowable torque of the shaft:

The diameter of these pins must be given to determine the cross sectional area and the resulting shear stresses in the pins. From the final design geometry of the concept we have:

Analysis of this concept must also take into account the shear forces acting on the pins that hold the disks in place. If these forces are too great within the operating torque limits, then the pins will shear before the torque limiter even begins to compensate for any overloaded condition.

3.0 Shear Stress Analysis - Part 1 (pivoting pin on disk1)

And the spring constant is:

The distance from the point of contact of the spring to the pivoting axis of disk 1 must also be specified. However this distance will change as the disk is tilted. Using the distance between these two points when the disk is in a vertical position, this length can be calculated for any angle:

In equilibrium the Moment equation is equal to 0, therefore we can solve for the spring force.

The spring constant can then be found by

specifying the length that the spring must travel:

Therefore the required spring force to keep the disk at an angle during normal operation is: