The diameter of these pins must be given to determine the cross sectional area and the resulting shear stresses in the pins.

Analysis of this concept must also take into account the shear forces acting on the pins that hold the disks in place. If these forces are too great within the operating torque limits, then the pins will shear before the torque limiter even begins to compensate for any overloaded condition.

Shear Stress Analysis

And the spring constant is:

Therefore the required spring force to keep the disk at an angle during normal operation is:

The spring constant can then be found by

specifying the length that the spring must travel:

In equilibrium the Moment equation is equal to 0, therefore we can solve for the spring force.

Therefore it appears that a material may be chosen for the pins to withstand the shear

stresses involved.

And the Tensile yield Strength is:

For Type 301 cold rolled stainless steel:

In this case, this steel would not be suitable for the pins

However the Tensile yield Strength is:

For 1040 hot rolled steel The ultimate tensile strength is :

Depending on the material chosen for the pins, this design may or may not hold up to the required torque levels.

The shear force on the pins will depend on the angle of the disk and the Force from the maximum allowable torque of the shaft:

Given an angle of the disk with respect to the axis perpendicular to the axis of rotation of the shaft:

The geometry of the design will place a normal force on the second disk as a result of the force from the torque. Based on the angle of the disk this component of the force can be found. The reaction force from the second disc is equal to this force when the system is in equilibrium.

The Force located at this point on the

shaft can be calculated using the equation:

A tangential force will result on the end of the shaft

dependant on the radius of the point in question

For a given radius:

With a given torque limit:

Spring Force Analysis

Seizure Recovery System for Fuel System Distributor

Concept #4

The distance from the point of contact of the spring to the pivoting axis of disk 1 must also be specified. However this distance will change as the disk is tilted. Using the distance between these two points when the disk is in a vertical position, this length can be calculated for any angle:

The distance of the force acting on disk one from the pivoting axis of the disk

is found from the equation:

But first the distances d2 and d1 must be calculated

The width of the disks must be specified to find the

distance between the two pivoting axes of the disks

By analyzing the moment about the pivoting

axis of disk 1 we can solve for this spring force:

:

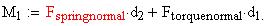
During normal operation this normal force is balanced by

a force from the spring in a direction that directly opposes it.

The normal force acting on the

disk from the spring is determined by: