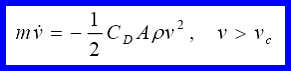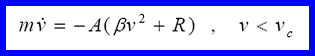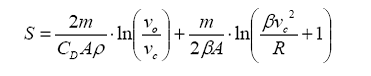
Soft Catch Background

Soft Catch-Background

When a projectile is every shot, it travels at an incredible velocity and is eventually stopped by some force. The size of the force is dependant on two factors; the velocity at which it is traveling and the mass of the projectile. Looking at Newton’s Second Law, two variables can be manipulated in order to get the desired result; force and time. If the projectile is stopped quickly, the force will be very large which will cause stress and deformation in the projectile . This experiment calls for the exact opposite. In order to have as little stress in the projectile as possible, a small amount of force can be applied over a large time interval in order to slow down the projectile. Recovering an undamaged particle is the purpose of a soft catch.

Deformed Projectile (Left) and Unfired Projectile (Right)

The soft catch is a useful tool in the field of ballistics. The recovery of the projectile can allow scientists and engineers to characterize the projectiles in either a legal sense or a metallurgical standpoint. For the Dynamic Tensile Test, the customer wishes to be able to recover the particles to view the grain properties of the material after the dynamic extrusion. The specimen in the test resembles an Explosively Formed Penetrator (EFP). Therefore, research on EFPs soft catches was examined.

According to the article supplied by the teams sponsor, a soft catch for EFPs was successfully constructed using a square channel lined with wood and filled with a variety of low density mediums. The diameter of the projectile was an inch while the length of the square was 12 inches. The soft catch was roughly 50 feet long with different compositions of various low density materials. This soft catch was not made by mistake or by random chance but based on some solid mathematical evaluation.

For any projectile, two separate equations of motion govern the particle. One of these controls the region above a critical velocity (V_c) and the other below. The two equations are shown below.

Drag Force Model Equation 1

Poncelet Form Equation 2

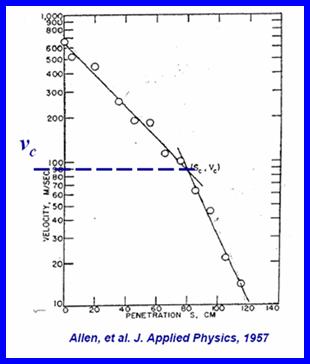
These two regimes are specific to the projectile and are found using experimental data (Shown Below)

Graph of Penetration vs. Velocity

After many data points are obtained, the points can be plotted to see where the inflection point occurs. The point corresponds to V_cand can help determine for later experiments which equation governs the particle at that instant. Some of the constants used in these equations are found through experimentation and are specific to each system.

More relationships can be found using the equations of motion in order to determine soft catch design. By taking the integral with respect to depth for both the Drag Force equation and the Poncelet equation, a single equation based on depth can be derived (Equation 3).

Penetration in Single Medium Equation 3

If the projectile is traveling at a speed largely above V_c