The Carnot Cycle

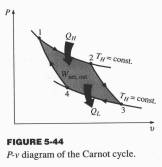
Carnot Efficiency

Consider an ideal gas undergoing a Carnot cycle between two temperatures TH and TL.

Ø 1 to 2, isothermal expansion, DU12 = 0

QH = Q12 = W12 = òPdV = mRTHln(V2/V1) (1)

Ø 2 to 3, adiabatic expansion, Q23 = 0

(TL/TH) = (V2/V3)k-1 (2)

Ø 3 to 4, isothermal compression, DU34 = 0

QL = Q34 = W34 = - mRTLln(V4/V3) (3)

Ø 4 to 1, adiabatic compression, Q41 = 0

(TL/TH) = (V1/V4)k-1 (4)

From (2) & (4): (V2/V3) = (V1/V4) Þ (V2/V1) = (V3/V4)

Since ln(V2/V1) = ln(V4/V3); substituting for ln(V4/V3) in (1)

Þ (QL/QH )= (TL/TH)

Hence: hth = 1-(QL/QH )= 1-(TL/TH)

It has been proven that hth = 1-(QL/QH )= 1-(TL/TH) for all Carnot engines since the Carnot efficiency is independent of the working substance.

Example: A typical steam power plant operates between TH=800 K (boiler) and TL=300 K(cooling tower). For this plant, the maximum achievable efficiency is 62.5%.