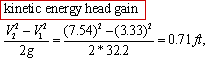|
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
|
|
Energy
conservation(cont.)
|
|
|
|
|
If energy is
added, removed or lost via pumps turbines, friction, etc.then we use
|
|
|
|
|
Extended
Bernoulli’s Equation
|
|
|
|
|
 |
Example:
Determine the efficiency of the pump if the power input of the motor
|
|
is
measured to be 1.5 hp. It is known
that the pump delivers 300 gal/min of water.
|
|
|
|
|
No turbine work
and frictional losses, hence: hE=hL=0. Also z1=z2
|
|
|
|
|
 |
Given:
Q=300 gal/min=0.667 ft3/s=AV
|
|
̃V1= Q/A1=3.33 ft/s V2=Q/A2=7.54
ft/s
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
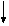 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
 |
|
|
|
|
|
|
|
|
|
|
Looking at
the pressure term:
|
|
|
|
 |
|
|
|
|
|
 |
|
|
|
|
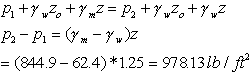 |
|
|
|
|
 |
 |
Mercury
(gm=844.9 lb/ft3)
|
water
(gw=62.4 lb/ft3)
|
|
1 hp=550 lb-ft/s
|
|
|
|
|
|
|
|