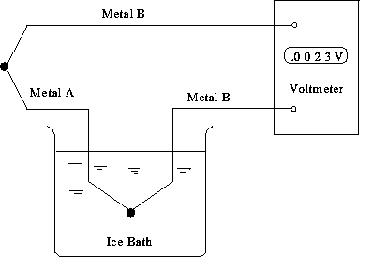
Figure 1 Measuring the EMF of a Thermocouple
Dynamic response of temperature
measuring device
(Transient heat transfer)
|
|
|
|
|
|
|
|
This experiment has two main goals. First, to introduce the basic operating principles of several common methods of temperature measurement such as, liquid-in-glass thermometers, thermocouples and thermistors and how to calibrate these devices. Second, to introduce the concept of dynamic response of thermal systems, ways of measuring this response and factors, which influence this behavior.
Temperature Measuring Devices
Thermocouples
When a pair of electrical conductors (metals)
are joined together, a thermal emf is generated when the junctions are
at different temperatures. This phenomenon is known as the Seebeck
effect. Such a device is called a thermocouple. The resultant
emf developed by the thermocouple is in the millivolt range when the temperature
difference between the junctions is ~ 100 0C. To determine the emf
of a thermocouple as a function of the temperature, one junction is maintained
at some constant reference temperature, such as ice-water mixture at a
temperature of 0 0C. The thermal emf, which can be measured by a
digital voltmeter as shown in Figure 1, is proportional to the temperature
difference between the two junctions. To calibrate such thermocouple
the temperature of the second junction can be varied using a constant temperature
bath and the emf recorded as a function of the temperature difference between
the two nodes.

Figure 1 Measuring the EMF of a Thermocouple
The output voltage, E, of a simple thermocouple circuit is usually written in the form,
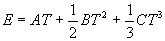 (1)
(1)
where T is the temperature in 0C, and E is based on a reference junction temperature of 0 0C. The constants A, B and C are dependent on the thermocouple material.
Providing a fixed reference temperature for the
reference junction using an ice bath can make the use of a thermocouple
cumbersome. Hence, commercially available thermocouples usually consist
of two leads terminating in a single junction. The leads are connected
to a thermocouple signal conditioning ‘box’ containing an electrical circuit
which provides a reference voltage equal to that produce by a reference
junction placed at 0 0C, a process called ‘ice point compensation’.
These thermocouple signal conditioners or ‘power supplies’ usually display
the temperature directly and or provide a voltage output that is proportional
to the thermocouple temperature. A similar thermocouple signal conditioner
with a digital temperature display and an analog voltage output is used
in the present experiment.
Thermistors
The thermistor, a thermally sensitive resistor, is a solid semi conducting material. Unlike metals, thermistors respond inversely to temperature, i.e., their resistance decreases as the temperature increases. The thermistors are usually composed of oxides of manganese, nickel, cobalt, copper and several other nonmetals. The resistance is generally an exponential function of the temperature, as shown in Equation 2:
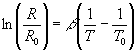 (2)
(2)
where R0 is the resistance at a reference temperature, T0, while b is a constant, characteristic of the material. T0, the reference temperature, is generally taken as 298 K (25 0C). Since all measurements made with thermistors can be reduced to detecting the resistance changes, the thermistor must be placed in a circuit and the resistance changes recorded in terms of the corresponding voltage or current changes. The formula relating the voltage (or current) changes to the resistance changes for a given circuit has to be determined theoretically or empirically, or by a combination of both.
In the design of thermistor circuits, one must take the precaution that within the range of the operating conditions, the circuit remains stable at all times. Thermistor resistance varies inversely with temperature. The voltage applied directly across a thermistor causes its temperature to rise, and its resistance to decrease. Sufficiently high voltage may cause thermal "runaway" (curve A in Figure 2), in which condition, higher currents and temperatures are induced until the thermistor fails, or the power is reduced. A series resistor, introduced to limit current, ensures stability (curve B). Thermal "runaway" will, in all probability, permanently damage the thermistor, or change its characteristic properties.
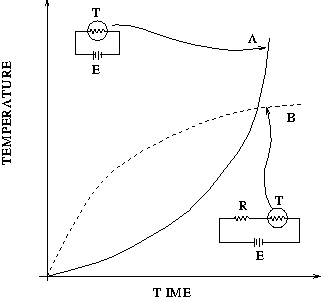
Figure 2 Thermistor Behavior and Thermal Runaway
To increase the precision of the measurement, one should add a voltage divider to the circuit shown in Figure 4(a). This will convert it to a Wheatstone bridge circuit, as shown in Figure 4(b). The out-of-balance voltage, DV, can then be measured and related to the resistance of the thermistor. A correct choice of resistors R2 and R3 will remove the mean DC value of DV. Note that although the bridge circuit can increase the precision of the readings, the sensitivity is still the same as for the simple voltage divider circuit shown in Figure 4(a). The simple DC bridge circuit of Figure 4(b) is generally satisfactory for most applications.
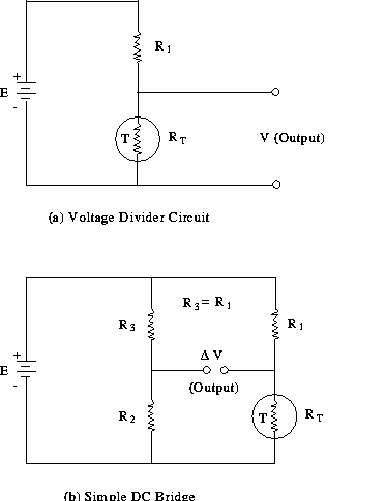
Figure 3 Thermistor Circuit
Considering this circuit, we shall now derive the relation between T and DV. In general,
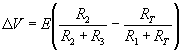 (3)
(3)
Assume R1 = R3. Then,
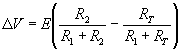 (4)
(4)
Rearranging for RT,
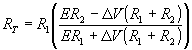 (5)
(5)
The relation between T and RT is given by,
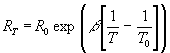 (6)
(6)
or,
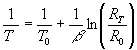 (7)
(7)
Substituting for RT from Equation 5, we have
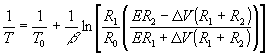 (8)
(8)
If we further assume R1 = R2 = R3 = Rb, we have,
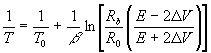 (9)
(9)
T is not a linear function of V, and so any linear
analog recorder will be in error when linear interpolation is used between
calibration points (for small ranges in temperatures, the error may be
negligible). If we measure E along with our scans of the DVs, then
the only unknowns in Equation 9 are R0 and b. These unknowns
are determined by calibration experiments. You will perform a 3 or 4 point
static calibration of both the thermocouple and the thermistor.
Back to the top
Dynamic Response of Thermal Systems
When temperature measurements of a transient process are made, it is important to verify that the dynamic response of the measuring device is fast enough to accurately track the time varying temperature. In the second part of this experiment, we will study the influence of different parameters on the transient response characteristics of a thermal system. In this experiment, we will measure the response of thermocouple (or a modified thermocouple). The thermocouple is modeled as a spherical ball, as shown in Figure 4. The thermocouple temperature is, T, mass m and specific
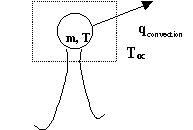
Figure 4 – Thermocouple bead modeled as a simple thermal system
The solution for the above first order equation is the well known exponential decay given as:
![]()
where the time constant t = mc/hA. In this experiment, we will examine the influence of properties suh as mass, surface area and specific heat capacity of the bead on its dynamic response.
The following apparatus is used in conducting the experiments:
1. Constant temperature bath: The constant temperature bath is capable of providing liquids at constant temperatures between approximately 10 to 90 0C. Several different temperatures will be used in the calibration procedure. Note how the settings are made and set the bath for a low temperature.
2. Thermocouples: The thermocouple used in this experiment is connected to a power supply, which has a digital temperature display and an analog output. The analog output is connected to the ADC card. The thermocouple will be calibrated by placing it in the constant temperature bath and recording the digital display and the voltage output using the computer and the ADC card.
3. Thermistor: Examine the thermistor provided; it will already be connected to a Wheatstone bridge circuit. You will calibrate it by placing it in the constant temperature bath along with the thermocouple and recording the output voltage. Thermocouples with different beads.
4. Wheatstone bridge circuit: For the thermistor.
5. Personal Computer and Analog-to-Digital (ADC) converter: This will be used to digitize and record the voltage signal form the thermocouple and thermistor as a function of time.
6. Resistance Temperature Detector (RTD): The RTD will be immersed in the constant temperature bath for the duration of the experiment. The temperature indicated by the RTD will serve as the reference temperature (i.e., actual temperature of the bath).
I. Thermocouple
and Thermistor Static Calibration
The static calibration for the thermocouple and
the thermistor will be done at the same time.
1. Connect the outputs of the thermocouples and the thermistor to the appropriate channels on the ADC card. Start the LabView program that is used for data acquisition. Ask the TA’s for assistance.
2. Place the thermocouple and the thermistor in the constant temperature bath. Place the in the constant temperature bath. Starting with the bath at the lowest setting, between 20 –0 0C.
3. Record the temperature of the RTD.
4. Record the thermocouple temperature and the voltage reading.
5. Record the thermistor out-of-balance voltage, DV, and
6. Repeat for three other different temperatures.
II. Time Response Measurement
1. Set the constant temperature bath between 20 and 40 0C.
2. Using the LabView program provided, monitor and record the outputs of the thermocouple as you rapidly move the thermocouple from the constant temperature bath and place them in the ice bath.
3. Now change the constant temperature bath temperature to somewhere between 60 and 80 0C and repeat step 2.
4. Without changing the constant bath temperature, repeat step 2 with the larger size “thermocouples”. Note the diameter and the material of all the thermocouple beads.
1. Discuss the principles of operation of thermocouples and thermistors. Compare the advantages and drawbacks of using the two devices.
2. Plot the static calibration data for the thermocouple and the thermistor, i.e. plot temperature vs. voltage. Does the voltage output confirm the expected trends? How and why?
3. Is the temperature in the constant temperature bath truly constant? Did you notice temperature fluctuations, and if so, what was their magnitude? What is the effect of these fluctuations on the accuracy of your static calibration?
4. Is there a discrepancy in the RTD temperature and the temperature displayed on the thermocouple digital display? Is the discrepancy constant over the entire temperature range? Discuss reasons for this discrepancy.
5. Determine the time constants for the smallest thermocouple at the two different temperature settings. Would you expect the time responses to be the same or different and why?
6. Determine and compare the time constants for
the larger diameter thermocouples. Keeping in mind the physical parameters
which govern the time response, is this trend expected?
Back to the top
![]()
Experiment 4 Data Sheet
Note: Please note the units
of the quantities which are being measured, when recording data.
For example,
when measuring voltage, if the voltmeter reads
16 mV, then write down 16 mV instead of just 16.
I. Inspect the constant temperature bath.
II. Thermocouple analysis:
1. Record output voltage of thermocouple:
Both terminals in air:_________
One terminal held between fingers and the other terminal in an ice bath:________
III & IV. Thermocouple and Thermistor calibration
1. Record the following:
a) Supplied voltage, E: __________
b) Wheatstone bridge resistor values:
R1 = _______________, R2 = ______________, and R3 = ______________
2. Place one junction
of the thermocouple in the ice bath and the other in the constant temperature
bath. Also place the
thermistor in the constant temperature bath. Record the temperature of
the
constant temperature
bath (via RTD), the thermocouple voltage (V) and the out-of-balance voltage
of the thermistor (DV)
in the following table. Repeat for ten different bath temperatures.
|
|
|
|
|
|
|
|||
|
|
|||
|
|
|||
|
|
|||
|
|
|||
|
|
|||
|
|
|||
|
|
|||
|
|
|||
|
|
|||
|
|
V: Time response:
DO NOT DISCONNECT THE WHEATSTONE BRIDGE CIRCUIT.
With the circuit in place, connect thermistor
(DV) output and thermocouple output to the ADC
card in the computer. The data will be recorded using a
LabView program, your lab TA will assist you
with this part of the experiment.
Note on Breadboard use:
The supplied breadboard should be used to develop
the wheatstone bridge circuit as discussed in the lab
handbook. The breadboard is simply a convenient
tool for building up circuits. The breadboard consists of
rows of small, electrically connected connection
points in a grid pattern. Interconnected connection points form
a bus. The board has three sections that
are divided to allow for easy circuit connection. Each section has
two
long buses running from top to bottom labeled
A and B. These buses are normally used for power connections
from the terminal posts located on the top of
the board or from the two long buses running left to right on the top
of the board (also labeled A and B). Small
buses consisting of five connection points are situated on the left
and right of the power bus. These buses
are only connected from left to right and are not connected to the
power bus. Each section of the board is
independent of the others. The breadboard configuration allows for
very complex circuits to be constructed and allows
for quick construction of the wheatstone bridge circuit
needed for this experiment. The supplied
wire set and resistors are pushed into the connection points in the
required configuration as illustrated in the
lab handbook. Consult the lab TA for further assistance.
YOU NEED TO GET THE LAB INSTRUCTOR'S SIGNATURE BEFORE LEAVING.
The student has performed the experiment satisfactorily
and has cleaned the work area.
___________________________ _______________
(Lab assistant's signature)
Date