Experiment 1


Properties of Thermal Radiation

Download  Experiment Description


Objectives
Theoretical Background
Apparatus
Experimental Procedure
Question to be Answered
Download Data Sheet

Objectives
 
The aim of this laboratory is to introduce the basic properties of thermal radiation .Through a series of simple experiments we will examine the emissive power of energy radiated by a body as a function of its temperature, its propagation through space and the temperature dependence of spectral distribution of thermal radiation.We will also investigate the emissivity of different surfaces and the transmission properties of glass as a function of temperature.

Theoretical Background

 
Thermal Radiation
Thermal radiation is the energy emitted by a body as result of its finite temperature.In contrast to heat transfer through convection and conduction, radiation heat transfer does not require a medium and can occur in a vacuum. This is because thermal radiation energy is a type of electromagnetic (E-M) radiation and like other types of E-M radiation it can travel can travel through vacuum at the speed of light. Since it is the only mode of heat transfer that can take place through vacuum, radiative heat transfer is the mode of heat exchange between the Sun and Earth; hence the term solar radiation.
 

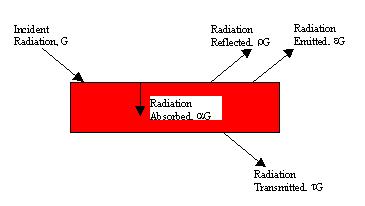
  Fig. 1 - Radiative properties of a surface






Fig. 1 shows that when radiant energy G (W/m2) is incident on a surface, portions of it can be reflected, absorbed and/or transmitted. The relative fractions that are reflected, absorbed and transmitted are determined by the radiative properties  r, a  and  t, the reflectivity, absorptivity and transmissivity, respectively, of that surface. From conservation of energy we also know that:

r + a + t = 1

In addition to the above, the surface also emits energy via radiation where the amount of energy emitted by the surface is given by the Stefan-Boltzmann Law:

                                                                                         E=esAT4
In this equation,  s  is called the Stefan-Boltzmann constant and is equal to 5.67 x10-8 W/m2K4; A is the surface are, e  is the emissivity of the surface, a surface property similar to r, a and t and T is the absolute temperature of the body in degrees Kelvin. The emissivity of a body can vary between 0 and 1. A surface with e = 1 is a perfect radiator and is referred to as a black body radiator; for all real surfaces, e < 1. The Stefan-Boltzmann law will be verified in this experiment.

 

Thermal Radiation Spectrum
 

Electromagnetic radiation, like all other forms of radiation, travels at the speed of light, which is related to its wavelength, l, and frequency n by

c=vl

where c = 3 x108m/s is the speed of light. Thermal radiation spans only a portion of the entire electromagnetic spectrum, which ranges from X-rays to Microwaves. The thermal spectrum spans

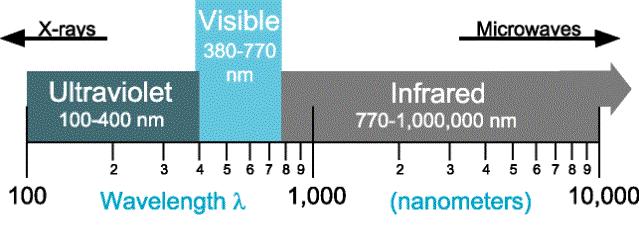
Fig. 2  Thermal radiation portion of the Electromagnetic Spectrum

(Courtesy of EML 3015, C. Shih)

a range of 0.1mm - 100mm, which, as shown in Fig. 2 includes the entire visible spectrum. Whether thermal radiation is visible, and at what color, is a function of the portion of the radiation that falls within the visible spectrum. Not only is the total amount of thermal radiation emitted by a surface  -  described by the Stefan-Botzmann’s law  -  a direct function of temperature, how this energy is distributed over the thermal spectrum as a function of wavelength, is also a related to the surface temperature.

The Planck Distribution gives the spectral distribution of thermal radiation of a Black Body as a function of temperature. This distribution function can be found in any standard undergraduate heat transfer text. Using Planck’s Distribution, the spectral distributions from black bodies at various temperatures are shown in Fig. 3. The figure shows that energy radiated varies continuously with wavelength at any given temperature. It also illustrates that at lower temperatures most of the energy the energy is outside the visible spectrum. However, as the temperature rises, more and more energy is shifted to shorter wavelengths and into the visible spectrum region. The dependence of spectral distribution on temperature also explains why the
 
 

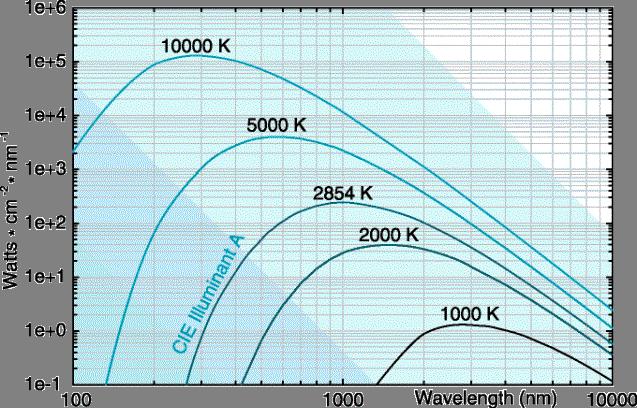
Fig. 2 – Spectral distribution of a Black body emissive power using Planck’s Distribution 

(adapted from EML 3015 notes by Dr. Shih)

color of a body changes as it is heated: from black to dark red to bright red to yellow and finally to white hot. The overall intensity of the visible light from an object also increases with temperature since a larger percentage of the total energy radiated is in the visible spectrum.

Solar radiation has a spectrum very similar to that of a black body at 5800K. As a result, a large portion of solar radiation is visible. The reflectivity, absorptivity and transmissivity of most materials are also a function of wavelength of the incident radiation. Hence they may transmit radiation from sources above (or below) certain temperatures, i.e. within a certain range of wavelengths, while blocking light from sources at temperatures outside that range. This wavelength dependence of material transmission properties is responsible for the greenhouse effect and will also be explored in this experiment.
 

Apparatus
 

The following main components will be used to conduct different parts of this experiment.
 

Stefan-Boltzmann Lamp:

This lamp will serve as a high temperature source of thermal radiation. By adjusting the voltage and current supplied to this lamp, filament temperatures as high as 3000°C can be obtained. The voltage and current supplied to this lamp can be monitored using a voltmeter and an ammeter, respectively. These values can be used to determine the resistances of the filament at various temperatures, which can then be used, calculate the temperature of the filament.

(IMPORTANT: Never supply more than 13V and 3A to this lamp)
 

Variable Power Supply:

This power supply will be used to operate the Stefan-Boltzmann lamp. Be very careful while using this supply, the current output is very high.

IMPORTANT: Never supply more than 13V and 3A to the lamp)
 

Radiation Sensor:

The Pasco TD-8553 radiation sensor produces a voltage output, which is proportional to the intensity of radiation incident upon the sensor. The output voltage ranges from microvolts to 100 millivolts.
 
 

Thermal Radiation (Leslie’s) Cube:

The cube has four different surfaces with different radiative properties. It can be heated up to temperatures of 120°C by a light bulb placed inside the cube. The cube temperature is measured by measuring the resistance of a thermistor embedded inside the cube. Once the resistance is measured the temperature can be obtained using the temperature vs. resistance calibration provided to you by the Teaching Assistants.

Multimeters:

Three multimeters will be provided to measure the voltages, currents, and resistances of the above components.
 

Experimental Procedure
 

NOTE: Please record all you measurements in appropriate tables or spaces in the data sheets.
 

I. Verification of Stefan-Boltzmann Law

The Stefan-Boltzmann Law will be verified in this experiment. You will also measure the transmission properties of glass as a function of temperature of the radiation source.
 

1. Connect the voltmeter, the ammeter and the Power supply to the Stefan-Boltzmann lamp as shown in Fig. 4 .

      Figure 4

The voltmeter should be connected to the binding posts of the lamp.

2. Connect the radiation sensor to a multimeter and place it approximately 6 cm away from the lamp, as shown.

3. Remove all other objects in the vicinity of the radiation sensor to ensure that its output is not influenced by extraneous radiation sources.

4. Before turning on the lamp, measure and record the ambient room temperature,Tref and the resistance of the lamp filament, Rref.

5. Turn on the power supply and set it to the lowest voltage reading, V, in Table 1 in the data sheet. Measure and record the current, I, and the radiation sensor output voltage.

6. Repeat step 5 for each voltage setting, V, in Table 1.

7. At V = 3 Volts place the glass square between the sensor and the bulb and record the radiation sensor output, repeat for V = 10 Volts.

Note: Record the sensor reading at each setting quickly. In between readings, cover the sensor with the insulating foam blocks provided. This prevents the sensor surface from overheating and providing erroneous readings.

Calculations for Determining the Filament Temperature

1. Determine the filament resistance, RT, at each voltage setting.

2. Divide the filament resistance, RT, by the reference resistance measured at room temperature, Rref to obtain RT /Rref.

3. Using either the table or the graph of RT /Rref as a function of temperature, determine the filament temperature.
 
 

II. Radiation Intensity as a Function of Distance

You will measure the magnitude of incident radiation on a surface as a function of distance from the thermal source in this experiment.
 

1. Arrange and connect the Stefan-Boltzmann lamp, the radiation sensor, the voltmeter and the power supply as shown in Fig. 5

Figure 5

 2.  Adjust the height of the sensor such that it is at the same level as the lamp filament.
 

 3.  With the lamp off, move the sensor to the relative distances, X, indicated in Table 2 of the data sheet
     (e.g. X = 2, 3, 4, 5, 10 cm …)
 4.  Measure and record sensor output voltage at each location in Table 2.
 5.  Now turn on the power to the lamp and adjust the voltage to approximately 10 volts. Please ensure that the current does not exceed 3A.
 6.  Move the sensor to the same X locations as in step 3.
.
 7.  Measure and record sensor output voltage at each location in Table 3.
Note: As before, record the sensor reading at each location as quickly as possible. In between readings, cover the sensor with the insulating foam blocks.
 
III Emissivity of Various Surfaces
 
1. Turn on the radiation cube to the HIGH power setting and monitor the thermistor resistance. When the resistance reaches 40 KW, change the power setting to 5. See Fig. 6 for a sketch of the setup.

Figure 6

2. Once the cube has reached equilibrium conditions at a power setting of 5, place the radiation sensor such that its two prongs are touching one of the cube surfaces. You will know that the cube has reached equilibrium conditions when the resistance fluctuates around a fixed value.

3. Record the sensor output voltage in Table 4 . Repeat this with the sensor facing each of the four surfaces. Also record the thermistor resistance; this will be used to obtain the thermistor temperature.

4. Repeat steps 2 and 3 for power settings of 7 and 9. At each new setting wait for the cube to reach equilibrium conditions.

Note: As before, to prevent the sensor from heating up, cover the sensor with the insulating foam blocks, in between readings.
 

Questions to be answered

I. Verification of Stefan-Boltzmann Law

1. Plot the measured measured radiation as a function of T4.  Is this relationship linear over the entire range of measurements? If not, discuss the reasons for this non-linear behavior.

2. The Stefan-Boltzmann Law is exactly applicable for perfect black bodies. Do your results indicate that the light bulb behaves as an ideal black body?  If it does, over what temperature range, discuss reasons for departure from black body behavior.

3. Compare the radiation sensor output at the voltages with and without the glass plate.  Is glass a better transmitter of radiation at higher or lower temperatures and why?

4. In light of the results discussed in question 3, what is the link between this behavior and the Greenhouse Effect.  Also, does it explain why the inside of a car parked in the sun heats up so rapidly?

II. Radiation Intensity as a Function of Distance

1. Plot the net radiation from the source, i.e. radiation with lamp on – radiation with lamp off, as a function of distance.  Discuss reasons for the trend observed in this plot, e.g. if it is linear or exponential, etc. and why.

2. If the plot in question 1 is not linear, plot the net radiation as a function of 1/X2.  It is known that radiation from a point source decays linearly with distance squared.  Explain this observation.  Does your plot support this assertion over the entire range of measurements?

III. Emissivity of Various Surfaces

1. List the four surfaces of the Leslie’s Cube in terms of emitted radiation in descending order. Is this order dependant on the source temperature (voltage)?

2. For all three experiments, lists some sources of error that might have affected your measurements.  Briefly discuss the effect and significance of these sources on your results.
 

Reference:

“Introduction to Thermodynamics and Heat Transfer,” Yunus A. Cengel, Chapter 12: Radiation and Heat Transfer, McGraw Hill, 1997, pp.  625 – 700.