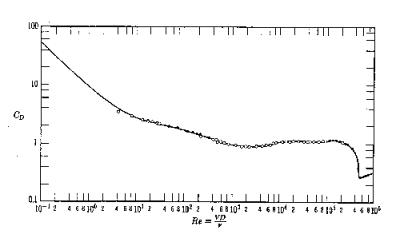
Aerodynamics
of Flow Around a Cylinder
| Objective | ||
| Experimental Procedure | Questions to be Answered | Download Data Sheet |
where W is the width of the body and u1 denotes the velocity profile in the wake measured at Section I.
Unfortunately, the flow cannot relax to the free stream pressure, where p1 = p¥unless the measuring station is placed very far downstream of the cylinder, usually more than 100 diameters. It is therefore not realistic to obtain measurements at section I.Nevertheless, it is possible to establish the relationship between the flow quantities measured at the hypothetical section I and those measured at actual section II which is located close to the cylinder.The procedure is as follows:
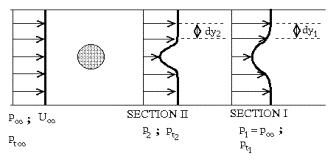
Figure
1.
Sketch of the test setup.
In
order to find the relation between FD
and the velocity profile at the designated measuring station II, we apply
the continuity equation, equation 2, along a stream tube
![]() (2)
(2)
Hence,
it follows that:
![]() (3)
(3)
Furthermore,
we make the assumption that the flow moves from Section II to I without
pressure losses, i.e., the total pressure remains constant along each streamline
between I and II:
We can rewrite equation 3 by using equations 4 and 5.Hence, we have:
![]() (6)
(6)
where
the integral extends over cross-section II.
Introducing
a dimensionless drag coefficient, CD,
as follows :
![]() (7)
(7)
where
Wd is the reference area of the body, we can rewrite Equation
6 as follows:
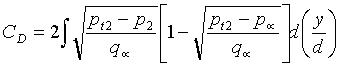 (8)
(8)
where
![]() (9)
(9)
![]() (11)
(11)
where
the integrations are taken around the contour of the cylinder. A cylindrical
coordinate will be used instead, and we can rewrite equation 11 as:
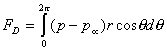 (12)
(12)
where
r is the radius of the cylinder, p is the pressure, q
is the angular position, and the integration is taken around the cylinder,
starting from the stagnation point.
Similarly,
the lift force can be estimated as:
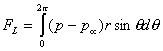 (13)
(13)
Apparatus
The
following components will be used:
1.
Wind Tunnel.
2.
Pitot-static tube (see description below).
3.
A cylindrical test model with circumferential pressure ports (see description
below).
4.
Scanivalve and scanivalve digital interface unit.
5.
ADC Card on a Pentium-based PC.
6.
Computer-controlled vertical drive.
Pitot-Static
Tube
A
pitot tube can be used in the wind tunnel to measure the velocity of the
tunnel. The assumption we have to make is that the static pressure is constant
everywhere in a uniform free-stream inside the wind tunnel. This is a reasonable
assumption considering that there is no pressure loss, therefore, no pressure
gradient, in the system. However, the situation will be very different
for measurements taken inside a wake behind a bluff body where a significant
amount of pressure variation exists across the wake profile. In order to
accurately determine the velocity profile in the wake, a pitot-static tube
should be used. The pitot-static tube, a sketch of which is shown in Figure
2, is a combination of the static tube and the pitot tube, which works
in the following manner. Assume that the tube is properly aligned with
the flow direction.If we further
assume that the flow is steady, one-dimensional, incompressible and inviscid,
all of which are very good assumptions under most conditions, we can derive
the following from Bernoulliís equation:
where
V is flow velocity, r
is the density of the fluid, pstag
is the stagnation pressure of the free-stream and pstag
is the static pressure.
WARNING:Start
the wind tunnel at a counter setting of 100 to 200 only. Do not start it
at higher counter settings
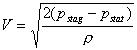
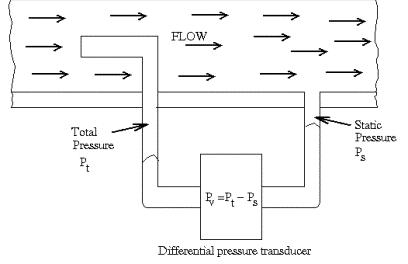
Figure
2. Pitot-static tube
Cylindrical
Test Model
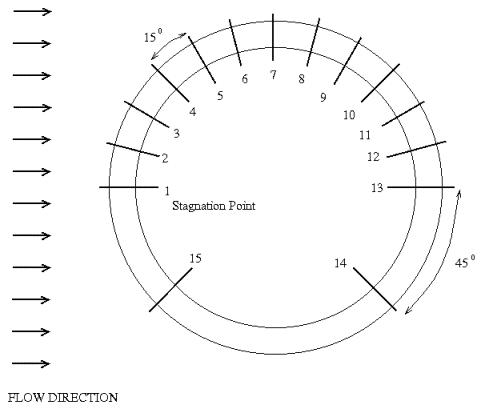
Figure
3. Pressure port locations
on the test model
1.Wake
Measurement:
Select two downstream locations, x/D = 5 and x/D=10 for the measuring section II.Set the wind tunnel speed counter at 550.
(a)Insert
the pitot, or pitot-static, tube into the wind tunnel upstream of the bluff
body. Measureand record the dynamic
pressure upstream of the body.
(b)
Remove the pitot tube from the upstream.
(c)
Move the pitot-static tube to the x/D=5 location.Center
it at the center of the cylinder.
(d)
Using the computer, measure the ADC output. Record this value.
(e)
Switch reference to P2.
(f)Using
the computer, move the pitot-static tube vertically upwards by 1 step.Each
step moved
by
the pitot-static tube using the computer constitutes a movement of 4 mm.
(g)
Measure and record the ADC output at this point.
(h) Repeat the measurement procedure for a total of 26 steps, i.e. a total travel distance of 100 mm.
(i)
Move the pitot-static tube to the x/D=10 location.Center
it at the center of the cylinder.
(j)
Repeat the measurement procedure followed for the x/D=5 location.
2.
Normal Pressure distribution:
Two
different Reynolds numbers shall be used for this part of the experiment.Wind
tunnel speed counter settings of 550 and 350 will be used to obtain the
two different Reynolds number.
(a)
Set the wind tunnel speed counter at 550.
(b)Using
the scanivalve, select the port # 2 on the scanivalve digital interface
unit (SDIU).This
corresponds
to the port # 1 on the Figure 3.
(c)
Using the computer, measure and record the ADC output
(d) Step through to the next port on the SDIU.
(e)
Repeat Step 2c.
(f)
Go through this process for all the ports, i.e., up to port 16 on the SDIU.
(g)
Set the wind tunnel speed counter at 350.
(h)
Repeat Step 2b through to Step 2f