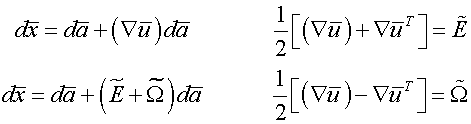
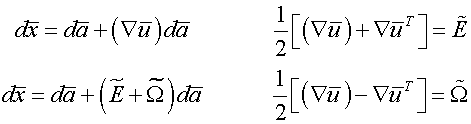
is
stretched and rotated to result in
.
Stretching comes purely from
,
whereas the rotation comes both from
and
.
However, if
is
along the eigen vector direction of
,
then change (rotation) in
comes
purely from
Thus
denotes
the rotation of eigen vector of
.
If
is
dual vector of
,
then
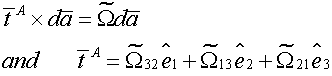
where
lie along the principal direction
of
.
Next: 3.12 Time Rate of Change of a Material Element
10/02/01 0:11:04