Recall
that
, where
is the original vector between two
points, and
the vector after deformation. If
is a pure
, then
have same length, i.e., no strain but rigid body motion.
It is likely that in a body some parts are subjected to
pure strain, pure rotation, or a combination of the two. To compute the
strain, all the rigid motion effect should be eliminated.
If
is symmetric, let
be designated as
, then
In
the neighborhood of
, there is only pure stretching. Since
is real and symmetric,
can be made diagonal with specific
corresponding to
,
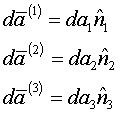
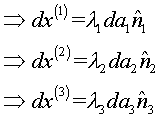
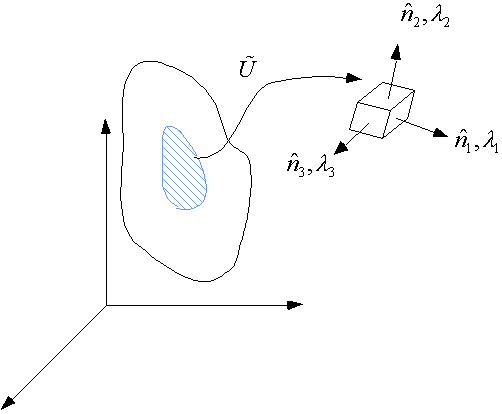
Let
stretch
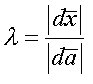
Thus
eigen values of
are the principal stretches
(minimum, intermediate, maximum)
10/02/01 1:04:09 10/04/01 0:00:24