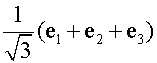Problem 2B8 (page 70)

Problem:

   Consider a plane of reflection which passes through the origin. Let n be a unit normal vector to the plane and let r  be the position vector for a point in space

(a)     Show that reflected vector for r  is given by Tr=r-2(r.n)n, where T  is the transformation that corresponds to the reflection.

(b)     Let n= 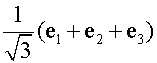, find the matrix of linear transformation that corresponds to this reflection

(c)     Use this linear transformation to find the mirror image of a vector

Answer:

(a)     Let T be the transformation and and  be the normal and the tangential components of the vector r. These components are given by and .  Then, in a reflection,

(b) 

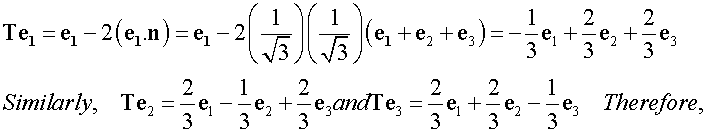
(c)