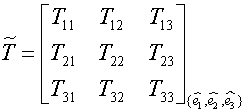
Previous: prob4-23>> Problem 4.23
Consider the state of stress given by
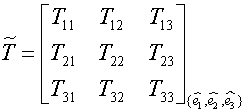
is symmetric. When we determine the principal value, let
and
be
the principal value. Let
and let
the eigen vectors
,
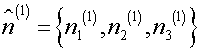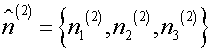
and
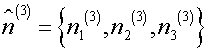be associated with
and
Note that
form
a rectangular Cartesian coordinate system. If [Q] represents the transformation
from
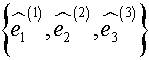to
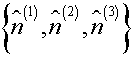, then
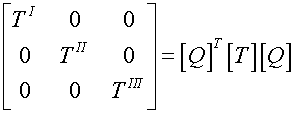
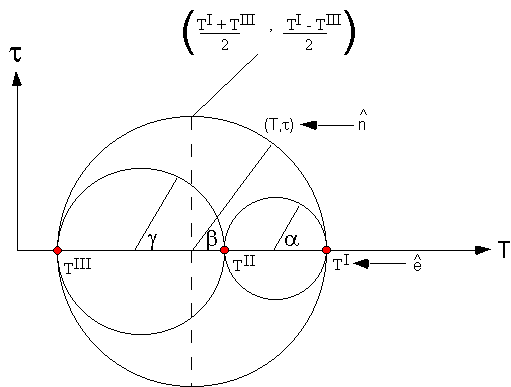
X-axis represents the eigen value with coordinate system
.
As we rotate the radius with arbitrary angles a,
b
and g
with old system (eigen vector system) with
Thus
Thus Mohr's circle in three dimensions is the coordination transformation of any orientation of the stress cube from the cube when aligned with the principal orientation lying along the x-axis.
10/18/01 0:53:51 10/23/01 0:00:51