5.2 Linear Elastic Solid

 Previous:  5.1(b) The Elastic Solid and Elastic Boundary Value Problems

If is Cauchy tensor and is small strain tensor, then in general,

where is the fourth order elasticity tensor, since  is a tensor,

However, we know that   then

 We have  symmetric matrix with 36 constants,

If elasticity is a unique scalar function of stress and strain, strain energy is given by

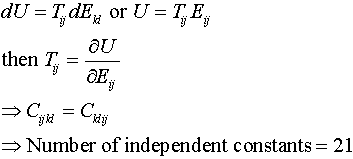
Now consider that there is one plane of symmetry (monoclinic) material, then

    One plane of symmetry 13

If there are 3 planes of symmetry, it is called an ORTHOTROPIC material, then

    orthotropy 3 planes of symmetry 9

Where there is isotropy in a single plane, then

    Planar isotropy  5 

When the material is completely isotropic (no dependence on orientation)

    Isotropic  2

Next:  Chapter 5 Overview

10/30/01 0:26:08