18.8.3.1 Solution 2dcanel-a

Question:

Convert the equation

$$10 u_{xx} + 6 u_{xy} + 2 u_{yy} = u_x + x + 1$$

to two-di­men­sion­al canonical form.

Using rotation and stretching of the coordinates you would get

$$u_{\xi\xi} + u_{\eta\eta} = \frac{3}{\sqrt{110}} u_{\xi} - \... ...frac{3\sqrt{11}}{\sqrt{10}} \xi - \frac{1}{\sqrt{10}} \eta + 1$$

Do you get the same equation? Should you? Comment.

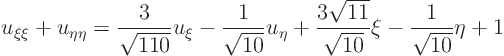
Answer:

You get

$$u_{\xi\xi} + u_{\eta\eta} = \frac{3}{11} u_{\xi} + \frac{1}{... ...t{11}} u_{\eta} + \frac{100}{11\sqrt{11}} \eta + \frac{10}{11}$$

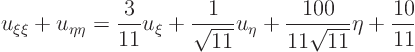
You do not necessarily get the same result. If you rotate the coordinate system, the Laplacian stays the same, but the right hand side changes. The same happens when you scale both coordinates by the same factor.