18.6.2.1 Solution clasnd-a

Question:

The equation

$$u_t - \nabla\cdot(p \nabla u) + q u = f$$

is a generic unsteady heat conduction equation, with 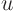$u$ the temperature relative to the surroundings. The first term is the rate of temperature change at a point. The second term represents heat accumulation at the point due to conduction of heat. In it, 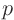$p$ is the heat conduction coefficient. The third term would in be an approximation to the heat radiated away to the surroundings, either in two-dimensions or for a transparant medium. The right hand side represents heat that is explicitly added from other sources. Classify this equation. Also classify the steady version, i.e. the equation without the 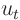$u_t$ term.

Answer:

Note that the unsteady equation is a partial differential equation in four dimensions even though there are no second order derivatives involving time. There is still a first order time derivative.