|
|
|
|
Next: 18.8 Two-Dimensional Coordinate Transforms |
|
Question:
Convert the equation
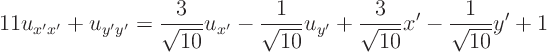
Answer:
Define ![]()
![]()
![]() ,
, ![]()
![]()
![]() to give
to give
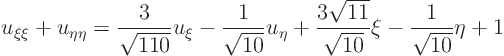
Then define ![]() by the relation
by the relation ![]()
![]()
![]() . Plug it in and you see that for the values of
. Plug it in and you see that for the values of ![]() and
and ![]() for which the first order derivatives vanish,
for which the first order derivatives vanish,