| Analysis Solution Manual |
|
© Leon van Dommelen |
|
18.3.1.2 Solution ppc-b
Question:
Assuming that the Dirichlet boundary-value problem for the Laplace equation on a finite domain,
is solvable, show that it depends continuously on the data.
Answer:
Assume that data 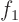 produce a solution
produce a solution 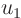 and
and 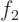 a solution
a solution 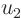 . Define
. Define 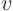 as the difference between the two solutions, and
as the difference between the two solutions, and 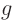 as the difference between the two data.
as the difference between the two data.
Show that 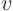 satisfies the Laplace equation. Show that on the boundary
satisfies the Laplace equation. Show that on the boundary 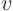 equals the change in the data
equals the change in the data 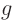 . Then, using the maximum and minimum properties of the Laplace equation, argue that the (maximum) change in the solution is no larger than the (maximum) change in the data.
. Then, using the maximum and minimum properties of the Laplace equation, argue that the (maximum) change in the solution is no larger than the (maximum) change in the data.
![]() produce a solution
produce a solution ![]() and
and ![]() a solution
a solution ![]() . Define
. Define ![]() as the difference between the two solutions, and
as the difference between the two solutions, and ![]() as the difference between the two data.
as the difference between the two data.
![]() satisfies the Laplace equation. Show that on the boundary
satisfies the Laplace equation. Show that on the boundary ![]() equals the change in the data
equals the change in the data ![]() . Then, using the maximum and minimum properties of the Laplace equation, argue that the (maximum) change in the solution is no larger than the (maximum) change in the data.
. Then, using the maximum and minimum properties of the Laplace equation, argue that the (maximum) change in the solution is no larger than the (maximum) change in the data.