18.3.3.2 Solution ppe-b

Question:

For the Laplace equation

$$u_{yy}+u_{xx}=0$$

with boundary conditions

$$u(x,0)=f(x)\quad u_y(x,0)=0 \quad u(0,y)=0 \quad u(\pi ,y)=0$$

the separation of variables solution is

$$u(x,y) = \sum_{n=1}^\infty f_n \sin(nx) \cosh(ny)$$

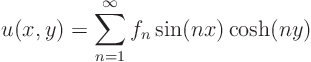
Here the Fourier coefficients $f_n$ must chosen so that they satisfy

$$f(x) = \sum_{n=1}^\infty f_n \sin(nx)$$

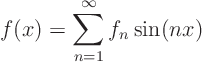
Check this solution.

Can you immediately see that this separation of variables solution is probably no good?

Answer:

Plug the solution in the partial differential equation and all four boundary conditions. You will find that they are all satisfied.

If you are concerned about manipulating infinite sums, then for now simply assume that $f(x)$ is such that $f_n$ is zero above some largest value $n$ $\vphantom0\raisebox{1.5pt}{$=$}$ $n_{\rm {max}}$. Then the sums are finite and you can manipulate them in the usual ways.

You can see that this separation of variables solution is probably no good, but not from the simple checks above. So no.