18.3.3.4 Solution ppe-d

Question:

Continuing the previous question, show analytically that for the supposed solution

$$u(x,y) = \sum_{n=1}^\infty\frac{4}{\pi n^2} \sin\left(n{\textstyle\frac{1}{2}}\pi\right) \sin(nx) \cosh(ny)$$

the sum does not converge for any $x$ if $y$ $\raisebox{.3pt}{$>$}$ 0.

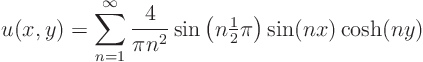
Also show analytically that at the halfway point $x$ $\vphantom0\raisebox{1.5pt}{$=$}$ $\frac 12\pi$, the values that you get while summing increase monotonically to infinity.

Answer:

Note that a requirement for a sum to converge is that the terms in the sum go to zero. Now apply good old l’Ho[s]pital, or equivalent, on $\cosh(ny)/n^2$.

At the halfway point, you can show that the terms being summed are always positive, and that they grow bigger and bigger. So their sum grows bigger and bigger too. Therefore $u$ goes to infinity monotoneously.