18.3.4.2 Solution pph-b

Question:

For the brave. Show without peeking at the solution that the problem for irrational $T$ is improperly posed by showing that you can make

$$\sin(nT\pi)$$

arbitrarily small by choosing suitable values of $n$. Then for these values of $n$, the solution

$$u = \frac{1}{\sin(nT\pi)}\sin(nx)\sin(nt)$$

becomes arbitrarily large in the interior although is is no larger than 1 on the boundary. So the problem for irrational $T$ is improperly posed too, but not because the solution is not unique, but because small data ($f$, i.e. $u$ on the top boundary) do not produce correspondingly small solutions in the interior.

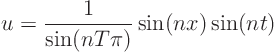
Answer:

Trying to approximate $T$ by its decimal expansion, as done for $\sqrt{2}$, is not accurate enough.

Instead note that what you need is that $nT$ is arbitrarily close to an integer. That will make the sine arbitrarily small.

To achieve that, build up the desired value of $n$ in stages as a product.

To start, simply take $n$ $\vphantom0\raisebox{1.5pt}{$=$}$ 1. Note that obviously $nT$ $\vphantom0\raisebox{1.5pt}{$=$}$ $T$ will always within a distance of no more that $\frac 12$ of some integer. Now if $nT$ is also within a distance of no more that $\frac 13$ of that integer, do not change $n$, leave it 1. If however the value of $nT$ is more than $\frac 13$ away from the integer, multiply $n$ by 2, i.e. take the new $n$ equal to 2. That brings the new $nT$ within $\frac 13$ of a (different) integer.

Next, if the current $nT$ is a distance within $\frac 14$ of an integer, do nothing. Otherwise multiply the current $n$ by 3. That brings $nT$ within a distance $\frac 14$ of an integer.

Next, if the current $nT$ is a distance within $\frac 15$ of an integer, do nothing. Otherwise multiply the current $n$ by 4. That brings $nT$ within a distance $\frac 15$ of an integer.

Etcetera. In this way, $nT$ can be driven arbitrarily close to an integer. That makes $\sin(nT\pi)$ arbitrarily small.