18.2.1.4 Solution stanexl-b2

Question:

Suppose you have a Laplace equation problem where the boundary is symmetric around the $y$-axis, like, say, in the previous two problems. In general, such a symmetric boundary means that if $(x,y)$ is a boundary point, then so is $(-x,y)$. Also assume that $u$ is given as an antisymmetric function of x on this boundary; $u(-x,y)$ $\vphantom0\raisebox{1.5pt}{$=$}$ $-u(x,y)$ for any boundary point. Show that in that case, $u$ is antisymmetric function of $x$ everywhere, i.e. $u(-x,y)$ $\vphantom0\raisebox{1.5pt}{$=$}$ $-u(x,y)$ everywhere.

Then show that this means that the solution $u$ will be zero on the $y$ axis.

Also explain why the above would no longer be true if you had a first order $x$ derivative in the PDE, like for example $u_{xx}+u_{yy}+u_x$ $\vphantom0\raisebox{1.5pt}{$=$}$ 0.

Answer:

To show that $u$ is zero on the $y$-axis if it is antisymmetric in $x$ is easy. Just apply $u(-x,y)$ $\vphantom0\raisebox{1.5pt}{$=$}$ $u(x,y)$ at $x$ $\vphantom0\raisebox{1.5pt}{$=$}$ 0 to get $u(0,y)$ $\vphantom0\raisebox{1.5pt}{$=$}$ $-u(0,y)$. Then note that something can only be equal to its negative if it is zero.

However, it is suprisingly messy to show that $u$ is indeed antisymmetric everywhere if it is on the boundary. To do it, define a couple of new variables:

$$\bar x = -x \qquad\bar u(\bar x, y) = - u(x,y)$$

Here $\bar{x}$ is the $x$-coordinate flipped over around the $y$-axis, and $\bar{u}$ is $u$ with its sign flipped over.

Graphically, this may be pictured as follows:

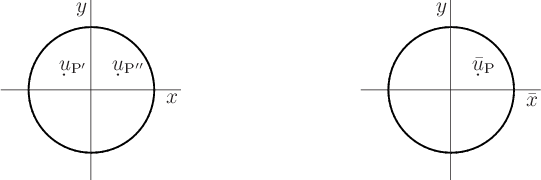
In terms of this picture, $\bar{u}$ at a point P in the $\bar{x},y$-plane is defined as $-u$ at the point P' in the $x,y$-plane.

Show that $\bar{u}(\bar{x},y)$ satisfies the Laplace equation just like $u(x,y)$. To do so, use the chain rule in

$$\bar u(\bar x, y) = - u(x,y)$$

where $x$ is a function of $\bar{x}$ given by $x$ $\vphantom0\raisebox{1.5pt}{$=$}$ $x(\bar{x})$ $\vphantom0\raisebox{1.5pt}{$=$}$ $-\bar{x}$.)

Show also that $\bar{u}(\bar{x},y)$ satisfies the exact same boundary condition as $u(x,y)$, (in terms of $\bar{x}$ of course.)

Then, since Dirichlet boundary value problems for the Laplace equation have unique solutions, $\bar{u}(\bar{x},y)$ must be the exact same function as $u(x,y)$. In terms of the picture above, $\bar{u}$ at the point P is the same as $u$ at the point P''. Since from the original definition it is also equal to $-u$ at P', it follows that $u$ at P' is $-u$ at P''. So $u$ is antisymmetric.

To see that the above no longer holds when there is a first order $x$ derivative in the equation, just try to repeat the above analysis and then observe where it goes wrong.