18.2.1.9 Solution stanexl-e

Question:

Return once again to the problem of the second-last question.

The correct solution to this problem, that you would find using the so-called method of separation of variables, is:

$$u(x,y) = \sum_{\textstyle{n=1\atop n {\rm odd}}}^\infty\fra... ...tyle\frac{1}{2}}n\pi x)\cosh({\textstyle\frac{1}{2}}n\pi(1-y))$$

Verify that this solutions satisfies both the partial differential equation and all boundary conditions.

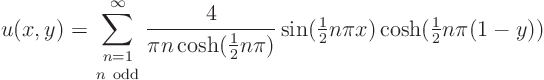
Now shed some light on the question why this solution is smooth for any arbitrary $y$ $\raisebox{.3pt}{$>$}$ 0. To do so, first explain why any sum of sines of the form

$$f(x)=\sum_{n=1}^\infty c_n \sin\left({\textstyle\frac{1}{2}}n\pi x\right)$$

is smooth as long as the sum is finite. A finite sum means that the coefficients $c_n$ are zero beyond some maximum value of $n$.

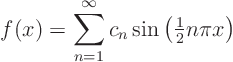
Next, you are allowed to make use of the fact that the function is still smooth if the coefficients $c_n$ go to zero quickly enough. In particular, if you can show that

$$\lim_{n\to\infty} n^k c_n = 0$$

for every $k$, however large, then the function $f(x)$ is infinitely smooth.

Use this to show that $u$ above is indeed infinitely smooth for any $y$ $\raisebox{.3pt}{$>$}$ 0. And show that it is not true for $y$ $\vphantom0\raisebox{1.5pt}{$=$}$ 0, where the solution jumps at the origin.

Answer:

Search through a table book, in the Fourier series section, for the following result:

$$\sum_{\textstyle{n=1\atop n {\rm odd}}}^\infty\frac{4}{\pi ... ... \le x\le 0$} \mbox{1 if $0\le x\le 2$} \end{array}\right .$$

The book might list this series in a slightly different form; in that case, just rescale the $x$ and $f$ values. If you can only find a saw-tooth, try differentiating it.

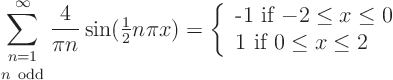
Using this result, you can show that the boundary condition at $y$ $\vphantom0\raisebox{1.5pt}{$=$}$ 0 is satisfied. The other boundary conditions and the partial differential equation can be verified directly from the form of the solution.

A single sine is an infinitely smooth function. You can differentiate it as many times as you want without getting singularities. Argue that according to calculus, the derivatives of a sum of two functions are just the sum of the derivatives of each separate function. So a sum of two sines is an infinitely smooth functions. And then so is the sum of a sum of two sines and another sine. And then so is the sum of the sum of three sines and another sine.

To show that the coefficients $c_n$ go to zero sufficiently quickly, you can use l’Ho[s]pital. You first need to compare $u$ with the generic $f(x)$ to see what the coefficients $c_n$ are that you want to be vanishingly small for large $n$.