18.2.3.2 Solution stanexw-b

Question:

Maxwell’s equations for the electromagnetic field in vacuum are

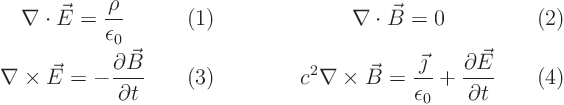
$\begin{displaymath} \begin{array}{ccccc} \displaystyle\nabla\cdot\vec E = \frac{... ...on_0} +\frac{\partial\vec E}{\partial t} & \quad(4) \end{array}\end{displaymath}$

Here $\vec{E}$ is the electric field, $\vec{B}$ the magnetic field, $\rho$ the charge density, $\vec\jmath$ the current density,

the constant speed of light, and $\epsilon_0$ is a constant called the permittivity of space. The charge and current densities are related by the continuity equation

$\begin{displaymath} \frac{\partial\rho}{\partial t} + \nabla\cdot\vec\jmath = 0 \qquad(5) \end{displaymath}$

Show that if you know how to solve the standard wave equation, you know how to solve Maxwell’s equations. At least, if the charge and current densities are known.

Identify the wave speed.

Answer:

Use the formulae of vector analysis, as found in, for example, [2].

First show from the Maxwell’s equations that the divergence of $\vec{B}$ is zero. Then vector calculus says that it can be written as the curl of some vector. Call that vector $\vec{A}_0$ .

$\begin{displaymath} \vec B = \nabla\times\vec A_0 \qquad(6a) \end{displaymath}$

Next define

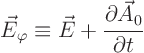
$\begin{displaymath} \vec E_\varphi\equiv\vec E + \frac{\partial\vec A_0}{\partial t} \end{displaymath}$

Plug it into the appropriate Maxwell’s equation to show that the curl of $\vec{E}_\varphi$ is zero. Then vector calculus says that it can be written as minus the gradient of a scalar. Call this scalar $\varphi_0$ . Plug that into the expression above to get

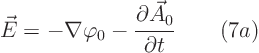
$\begin{displaymath} \vec E = - \nabla\varphi_0 - \frac{\partial\vec A_0}{\partial t} \qquad(7a) \end{displaymath}$

Next verify the following: if you define modified versions $\vec{A}$ and $\varphi$ of $\vec{A}_0$ and $\varphi_0$ by setting

$\begin{displaymath} \varphi = \varphi_0 - \frac{\partial\Omega}{\partial t} \qquad\vec A = \vec A_0 + \nabla\Omega \end{displaymath}$

where $\Omega$ is any arbitrary function of

, and

, then still

$\begin{displaymath} \vec B = \nabla\times\vec A \qquad(6) \end{displaymath}$

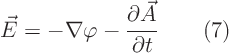
$\begin{displaymath} \vec E = - \nabla\varphi - \frac{\partial\vec A}{\partial t} \qquad(7) \end{displaymath}$

This is the famous gauge property of the electromagnetic field. Verify it by plugging in the given definitions of $\vec{A}$ and $\varphi$ and using (6a) and (7a).

Now argue that you can select $\Omega$ so that

$\begin{displaymath} \nabla\cdot\vec A + \frac{1}{c^2} \frac{\partial\varphi}{\partial t} = 0 \qquad(8) \end{displaymath}$

To do so, plug in the definitions of $\vec{A}$ and $\varphi$ to get

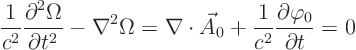
$\begin{displaymath} \frac{1}{c^2} \frac{\partial^2 \Omega}{\partial t^2} - \nabl... ...c A_0 + \frac{1}{c^2} \frac{\partial\varphi_0}{\partial t} = 0 \end{displaymath}$

Argue that this is an inhomogeneous wave equation for $\Omega$ . Argue that even if $\vec{A}_0$ and $\varphi_0$ do not satisfy (8), after you solve the wave equation for $\Omega$ , $\vec{A}$ and $\varphi$ will.

Now plug the expressions (6) and (7) for $\vec{E}$ and $\vec{B}$ in terms of $\vec{A}$ and $\varphi$ into the Maxwell’s equations. Clean up the expressions you get using (8). That gives uncoupled equations for $\vec{A}$ and $\varphi$ . Show that they are wave equations. Show that the wave speed is the speed of light.

So you have shown that for any solution $\vec{E}$ and $\vec{B}$ of Maxwell’s equations, there are potentials $\vec{A}$ and $\varphi$ that satisfy wave equations.

You will want to invert that argument. Suppose that you have solutions $\vec{A}$ and $\varphi$ of the wave equation. Suppose they satisfy (8). Show then that the $\vec{E}$ and $\vec{B}$ as defined by (6) and (7) satisfy Maxwell’s equations.