18.2.3.4 Solution stanexw-e

Question:

Return again to the problem of the last question. Assume $a$ $\vphantom0\raisebox{1.5pt}{$=$}$ 1.

The correct solution to this problem, that you would find using the so-called method of separation of variables, is:

$$u = \sum_{\textstyle{n=1\atop n {\rm odd}}}^\infty\frac{4}{... ...extstyle\frac{1}{2}}n\pi x)\cos({\textstyle\frac{1}{2}}n\pi t)$$

Verify that this solutions satisfies both the partial differential equation and all boundary and initial conditions.

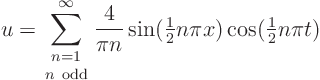
Explain that it produces the moving jump in the solution as given in the previous question.

The discontinuous solution given in the previous question is right in this case. It is right because it is the proper limiting case of a smooth solution that everywhere satisfies the partial differential equation. In particular, if you sum the above sum for $u$ up to a very high, but not infinite value of $n$, you get a smooth solution of the partial differential equation that satisfies all initial and boundary conditions, except that the value of $u$ at $t$ $\vphantom0\raisebox{1.5pt}{$=$}$ 0 still shows small deviations from $u$ $\vphantom0\raisebox{1.5pt}{$=$}$ 1. The more terms you sum, the smaller those deviations become. (There will always be some differences right at the singularity, but these will be restricted to a negligibly small vicinity of $x$ $\vphantom0\raisebox{1.5pt}{$=$}$ 0.)

Answer:

From the form of the solution, you will find that the partial differential equation, boundary conditions and initial condition on $u_t$ are satisfied. To verify the initial condition, found in Fourier series table books:

$$\sum_{\textstyle{n=1\atop n {\rm odd}}}^\infty\frac{4}{\pi ... ... \le x\le 0$} \mbox{1 if $0\le x\le 2$} \end{array}\right .$$

The table book might have this result in a slightly different form, but you can rescale it. You might want to give the function above a name, like $h(x)$.

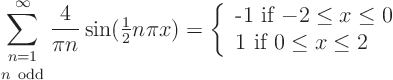
Now simplify the solution by using the fact that

$$\sin\alpha\cos\beta = {\textstyle\frac{1}{2}} \sin(\alpha +\beta) + {\textstyle\frac{1}{2}} \sin(\alpha -\beta)$$

This allows you to write the solution as the sum of two simpler ones. Each of these two terms can be written in terms of the function $h$ but with arguments $x-t$ and $x+t$ insteda of $x$.

Plot these two solutions in the same graph of $u$ versus $x$ for an arbitrary value of $t$ less than one and greater than zero. Add the two curves graphically together. Show in that way that $u$ $\vphantom0\raisebox{1.5pt}{$=$}$ 0 for $x$ $\raisebox{.3pt}{$<$}$ $t$ and $u$ $\vphantom0\raisebox{1.5pt}{$=$}$ 1 for $x$ $\raisebox{.3pt}{$>$}$ $t$. That is the solution as given in the previous question.