Up: Contents
Gram-Schmidt
Description:
Gram-Schmidt (or Gramm-Schmidt?) is a way of converting a given
arbitrary basis 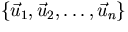 into an
equivalent orthonormal basis:
into an
equivalent orthonormal basis:
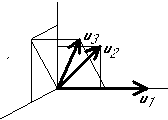
This often leads to better accuracy (e.g. in least square problems)
and/or simplifications.
Modified Gram-Schmidt Procedure
Start with the first vector, putting i=1. Now
- 1.
- Normalize vector
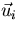 :
:
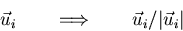
- 2.
- For the remaining vectors
 , eliminate their component in the directions of
, eliminate their component in the directions of 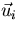 using the
following formula:
using the
following formula:

- 3.
- Increment i and repeat until there are no vectors left.
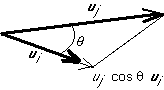
Note that for real vectors
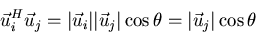
is indeed the component of  in the direction of
in the direction of 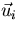 :
:
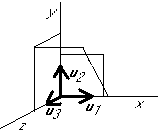
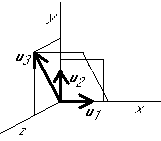
Graphical example:

Normalize  :
:
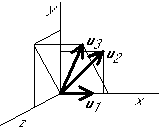
Eliminate the components in the  direction from the rest:
direction from the rest:
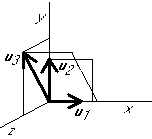
Normalize 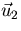 :
:
Eliminate the components in the 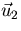 direction from the rest:
direction from the rest:
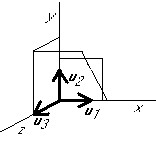
Normalize 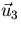 :
:

Projection:
The component substraction formula can also be read as
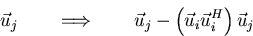
The matrix 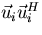 is the projection operator
onto
is the projection operator
onto 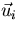
Up: Contents
 10/11/00 0:32:32
10/11/00 0:32:32
 10/11/00 0:35:18
10/11/00 0:35:18
 10/13/00 0:05:06
10/13/00 0:05:06
![]() into an
equivalent orthonormal basis:
into an
equivalent orthonormal basis:


![]()
![]()
![]()


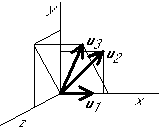


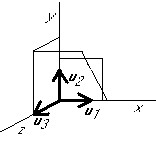

![]()