EML 5060 Homework Set 4 Fall 2001

Page HW Class Topic

33 3.22 intro

33 3.23 intro

35 3.38 intro

35 3.39 intro

35 3.40 intro. Use 3.37

35 3.41 intro

50 4.18 intro

50 4.19 intro

50 4.20

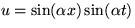17 2.19adh 2.19e Classification

17 2.20 Classification

17 2.21ac 2.21b Classification: assume u=u(x,y,z[,t])

18 2.25 2.24 Canonical form

18 2.26 Canonical form

18 2.22bef 2.22d Characteristics

18 2.27ae 2.27d 2D Canonical form

18 2.28bcjp 2.28nml 2D Canonical form

98 7.20 7.19 Unsteady heat conduction in a bar

98 7.21 7.22 Unsteady heat conduction in a bar

98 7.26 7.24 Unidirectional viscous flow

99 7.27 7.28 Acoustics in a pipe (use two methods)

99 7.35 7.36 Steady supersonic flow

99 7.37 7.37 Steady heat conduction in a plate

99 7.39 7.38 Potential flow inside a cylinder

00 Unsteady heat conduction in a disk

Also solve the following problem:

Solve the 2D unsteady vibrations 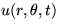of a circular membrane of radius r₀ if the membrane is fixed to a nonmoving drum at its perimeter, i.e. 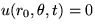. Use the separation of variables (eigenfunction expansion) method.

Initially, the membrane is at rest, but then at time t=0 it is hit by a drum stick a distance 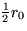away from the center. You may assume that the initial displacement 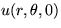of the membrane is still zero, but that the initial velocity is a delta function positioned at 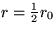and :.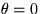

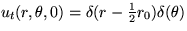To solve the problem, you are required to answer the following questions in the order asked (list question number with your answer):

1.

The governing P.D.E. is the two-dimensional wave equation 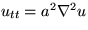where a is the given wave propagation speed. Write this equation out in polar coordinates.

2.

Identify the spatial domain of the problem.

3.

Identify the boundary conditions.

4.

Identify the initial conditions.

5.

You will need two eigenfunction expansions to reduce this P.D.E. in three variables, r, , and t, into ordinary differential equations with only a single variable. Do the first expansion first. There are three possibilities for this expansion:

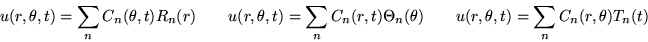
Only one of these three posibilities leads to a Sturm-Liouville problem after substitution of a single term into the P.D.E. and separating variables. Identify whether it is a Sturm-Liouville problem for R_n, 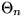, or for T_n. Since we do not want to give the solution away, from now on, we will indicate the right solution by X_n(x), and the remaining two variables (out of r, 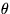, and t) by y and z. So the coefficients are now indicated as C_n(y,z).

6.

Write down the Sturm-Liouville problem for X_n(x) completely, including the boundary conditions. Solve it, or find a place where that problem has been solved before (same problem with same boundary conditions.)

7.

Find the transformation formulae that for an arbitrary funct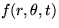ion produce the Fourier coefficients f_n(y,z) of that function in the eigenfunction expansion:

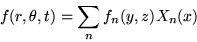
(In case the eigenvalues have double roots, there may actually be two such sums in the expansion for .)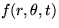

8.

Now that the eigenvalues of the first Sturm-Liouville problem have been found, you can write the equations satisfied by the C_n(y,z). (The other sides of the separated equations.) These will be P.D.E.s in the remaining two variables y and z (out of r, 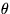, and t.)

9.

You will need the second eigenfunction expansion to reduce the P.D.E.s for the C_n(x,y) into ordinary differential equations with derivatives to only a single variables. There are two possibilities for this expansion:

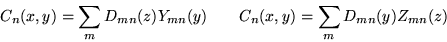
Only one of these two posibilities leads to a Sturm-Liouville problem after substitution of a single term into the P.D.E. and separating variables. Identify whether it is a Sturm-Liouville problem for X_mn or Y_mn. Since the definitions of y and z are arbitrary, from now on we assume it is an eigenvalue problem for Y_mn(y).

10.

Write down that Sturm-Liouville problem completely, including the boundary conditions. Solve it, or find a place where that problem has been solved before (same problem with same boundary conditions.)

11.

Find the transformation formulae that for an arbitrary function 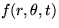with first Fourier coefficients f_n(y,z) produces the second Fourier coefficients f_nm(z) of the double eigenfunction expansion:

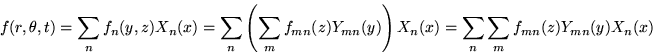
12.

Find the net transformation formulae that for an arbitrary function 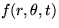produce the Fourier coefficients f_mn(z) of that function in the eigenfunction expansion above directly. (In terms of a multiple integral.)

13.

Solve the P.D.E. by expanding everything in it in terms of the double eigenfunction expansions obtained and solving the resulting O.D.E.

14.

Find the integration constants in the solutions of the O.D.E. by applying the given initial conditions. Please note that for Dirac delta functions

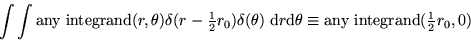
15.

What is the lowest frequency produced by the drum?