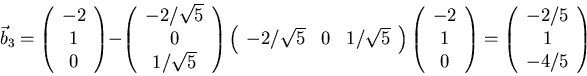Gram-Schmidt

Description:

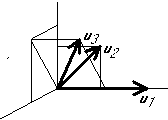
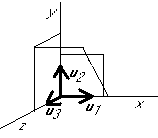
Gram-Schmidt (or Gramm-Schmidt?) is a way of converting a given arbitrary basis into an equivalent orthonormal basis:

This often leads to better accuracy (e.g. in least square problems) and/or simplifications.

Modified Gram-Schmidt Procedure

Start with the first vector, putting i=1. Now

1.

Normalize vector :

2.

For the remaining vectors , eliminate their component in the directions of using the following formula:

3.

Increment i and repeat until there are no vectors left.

Note that for real vectors

is indeed the component of in the direction of :

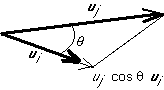
Graphical example:

Normalize :

Eliminate the components in the direction from the rest:

Normalize :

Eliminate the components in the direction from the rest:

Normalize :

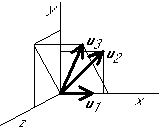
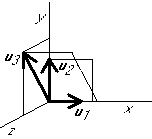
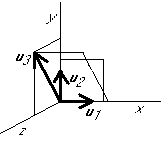
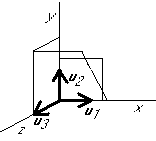
Projection:

The component substraction formula can also be read as

The matrix is the projection operator onto

Algebraic example:

Write the following matrix on principal axes:

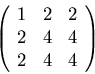
Eigenvalues are found to be , and . The eigenvector is directly found as (1/3,2/3,2/3), but for and we have the system of equations:

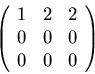
Initially taking each of the undetermined parameters 1, we get the two independent eigenvectors and , but they are not orthogonal. So we apply Gram-Schmidt.

Vectors a₂ and a₃ are already orthogonal to ,so substracting -components, as in and leaves them unchanged.

Normalizing gives .

Then substracting the -component from as in :

and normalizing that gives .

10/10/01 0:10:24