Up: Fall 2002
EML 5060 Homework Set 4 Fall 2002
| Page |
HW |
Class |
Topic |
| 33 |
3.22ade |
|
intro |
| 35 |
3.38 |
|
intro |
| 35 |
3.39 |
|
intro (see note 1 below) |
| 35 |
3.40 |
|
intro (see note 2 below) |
| 35 |
3.41 |
|
intro (see note 3 below) |
| 50 |
4.18 |
|
intro |
| 50 |
4.19 |
|
intro |
| 50 |
4.20 |
|
intro (see note 4 below) |
| 17 |
2.19cfg |
2.19e |
Classification |
| 17 |
2.20 |
|
Classification |
| 17 |
2.21ac |
2.21b |
Classification: assume u=u(x,y,z[,t]) |
| 18 |
2.25 |
2.24 |
Canonical form |
| 18 |
2.26 |
|
Canonical form |
| 18 |
2.22bf |
2.22d |
Characteristics |
| 18 |
2.27b |
2.27d |
2D Canonical form |
| 18 |
2.28egj |
2.28nml |
2D Canonical form |
| 98 |
7.20 |
7.19 |
Unsteady heat conduction in a bar |
| 98 |
7.21 |
7.22 |
Unsteady heat conduction in a bar |
| 98 |
7.25 |
7.24 |
Unidirectional viscous flow |
| 99 |
7.27 |
7.28 |
Acoustics in a pipe (use two methods) |
| 99 |
7.35 |
7.36 |
Steady supersonic flow |
| 99 |
7.37 |
7.37 |
Steady heat conduction in a plate |
| 99 |
7.39 |
7.38 |
Potential flow inside a cylinder |
| 00 |
|
|
Unsteady heat conduction in a disk |
Note 1: Guess the solution for x2+y2<1
Note 2: Use 3.37 with f nonzero only in 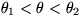 and see what part of the interior becomes nonzero.
and see what part of the interior becomes nonzero.
Note 3: Assume 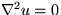 instead of 1. Then make a physical
argument based on the physical interpretation of steady heat
conduction in a circle with a heat flux 2 entering through the
perimeter.
instead of 1. Then make a physical
argument based on the physical interpretation of steady heat
conduction in a circle with a heat flux 2 entering through the
perimeter.
Note 4: Solutions must be of the form 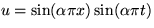 .See when they satisfy the given conditions.
.See when they satisfy the given conditions.
Also solve the following problem:
NO working together on the problem below! If you get stuck ask
the instructor or TA.
Solve the 2D unsteady vibrations 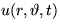 of a circular
membrane of radius r0 if the membrane is fixed to a nonmoving drum at
its perimeter, i.e.
of a circular
membrane of radius r0 if the membrane is fixed to a nonmoving drum at
its perimeter, i.e. 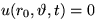 . Use the separation of
variables (eigenfunction expansion) method.
. Use the separation of
variables (eigenfunction expansion) method.
Initially, the membrane is at rest, but then at time t=0 it is hit
by a drum stick a distance 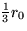 away from the center. You may
assume that the initial displacement
away from the center. You may
assume that the initial displacement 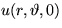 of the membrane
is still zero, but that the initial velocity is a delta function
positioned at
of the membrane
is still zero, but that the initial velocity is a delta function
positioned at 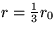 and
and 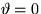 :
: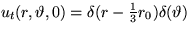 .
.
To solve the problem, you are required to answer the following
questions in the order asked (list question number with your answer):
- 1.
- The governing P.D.E. is the two-dimensional wave equation
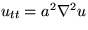 where a is the given wave propagation speed.
Write this equation out in polar coordinates.
where a is the given wave propagation speed.
Write this equation out in polar coordinates.
- 2.
- Identify the spatial domain of the problem.
- 3.
- Identify the boundary conditions.
- 4.
- Identify the initial conditions.
- 5.
- You will need two eigenfunction expansions to reduce this P.D.E.
in three variables, r,
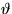 , and t, into ordinary
differential equations with respect to t only. These
expansions are similar to those of the heat conduction problem
covered in class, but not the same.
, and t, into ordinary
differential equations with respect to t only. These
expansions are similar to those of the heat conduction problem
covered in class, but not the same.
- 6.
- Write down the Sturm-Liouville problem for
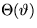 completely, including the boundary conditions by substituting a term
of the form
completely, including the boundary conditions by substituting a term
of the form 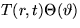 into the homogeneous PDE.
Solve it, or find a place in the lecture notes where that problem
has been solved before (same problem with same boundary conditions.)
into the homogeneous PDE.
Solve it, or find a place in the lecture notes where that problem
has been solved before (same problem with same boundary conditions.)
- 7.
- Find the transformation formulae that for an arbitrary function
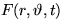 produce the Fourier coefficients Fin(r,t) of
that function in the eigenfunction expansion:
produce the Fourier coefficients Fin(r,t) of
that function in the eigenfunction expansion:
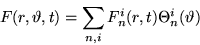
- 8.
- Now that an eigenfunction expansion in the
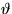 coordinate has been found, find a subexpansion in the r coordinate
by substituting a single term of the form Tin(t) Rin(r) into
the equation for the Tin(r,t). Make Rin satisfy the right
boundary conditions. Where is the Sturm Liouville problem different
from the problem solved in class? How does that affect the
solution?
coordinate has been found, find a subexpansion in the r coordinate
by substituting a single term of the form Tin(t) Rin(r) into
the equation for the Tin(r,t). Make Rin satisfy the right
boundary conditions. Where is the Sturm Liouville problem different
from the problem solved in class? How does that affect the
solution?
- 9.
- Find the transformation formulae that for an arbitrary function
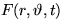 with first Fourier coefficients Fin(r,t) produces
the second Fourier coefficients Finm(t) of the double eigenfunction
expansion:
with first Fourier coefficients Fin(r,t) produces
the second Fourier coefficients Finm(t) of the double eigenfunction
expansion:
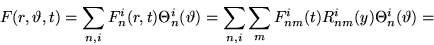
- 10.
- Find the net transformation formulae that for an arbitrary
function
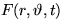 produce the Fourier coefficients
Finm(t) of that function in the eigenfunction expansion above
directly. (In terms of a multiple integral.) Where is it different
from the heat conduction problem?
produce the Fourier coefficients
Finm(t) of that function in the eigenfunction expansion above
directly. (In terms of a multiple integral.) Where is it different
from the heat conduction problem?
- 11.
- Expand everything in the PDE in terms of the double
eigenfunction expansions obtained and solve the resulting O.D.E.
for the uinm.
- 12.
- Expand everything in the IC in terms of the double eigenfunction
expansions obtained. While finding the Fourier coefficients of the
given initial conditions involves double integrals, they can
be found by noting that for Dirac delta functions the following is
true:
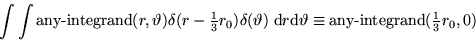
- 13.
- Work everything out as far as possible.
- 14.
- What is the lowest frequency produced by the drum? What is its
amplitude?
7.21 solution
7.37 solution
7.39 solution
Up: Fall 2002
![]() and see what part of the interior becomes nonzero.
and see what part of the interior becomes nonzero.
![]() instead of 1. Then make a physical
argument based on the physical interpretation of steady heat
conduction in a circle with a heat flux 2 entering through the
perimeter.
instead of 1. Then make a physical
argument based on the physical interpretation of steady heat
conduction in a circle with a heat flux 2 entering through the
perimeter.
![]() .See when they satisfy the given conditions.
.See when they satisfy the given conditions.
![]() of a circular
membrane of radius r0 if the membrane is fixed to a nonmoving drum at
its perimeter, i.e.
of a circular
membrane of radius r0 if the membrane is fixed to a nonmoving drum at
its perimeter, i.e. ![]() . Use the separation of
variables (eigenfunction expansion) method.
. Use the separation of
variables (eigenfunction expansion) method.
![]() away from the center. You may
assume that the initial displacement
away from the center. You may
assume that the initial displacement ![]() of the membrane
is still zero, but that the initial velocity is a delta function
positioned at
of the membrane
is still zero, but that the initial velocity is a delta function
positioned at ![]() and
and ![]() :
:![]() .
.![]()
![]()
![]()