Basis Changes

Student request: change notations. Mine seem better than the book's, though.

Suppose I have a basis S, .Then any arbitrary vector can be written as

where are the coordinates of in basis S. More briefly,

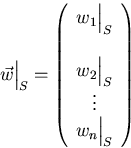
Suppose I have another basis S', .Then the same vector can also be written as

or

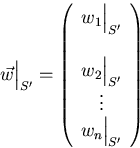
The relationship between the two sets of coordinates is always

where P is a matrix that is called the transformation matrix from S to S'.

Please note that this use of language is confusing: while P is called the transformation matrix from S to S', it really takes coordinates from S' and converts them to coordinates in S. Just the opposite of what you would expect.

In still other words, if you assume S is an ``old'' basis, and S' is a ``new'' basis you want to switch to, then the transformation matrix P from old to new really computes old coordinates from new ones. To get the new coordinates from the old ones, instead use Q=P^-1 (the transformation matrix from new to old):

Matrix P takes the form:

It contains the basis vectors of the S' system written in the S system. (That is why if I multiply with P, I get a vector in the S system.)

Warning: I think the books exposition (p207-210) is very confusing, partly by not using vector symbols to indicate vectors versus coordinates. I suggest you stick with my exposition above.

10/02/02 0:02:30 10/02/02 0:17:48