9.48(c), §2 Solution

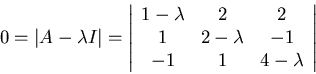
Eigenvalues:

There is a single root: and a double root

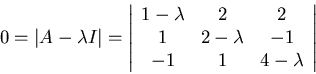
Eigenvectors corresponding to satisfy

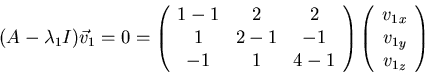
Solving using Gaussian elimination:

Equation (2') gives v_1y = -v_1z and then (1') gives v_1x = 2 v_1z.

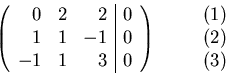
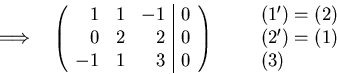
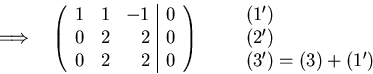
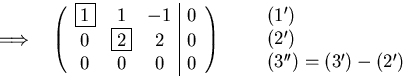
The general solution space is:

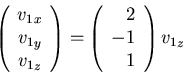
We choose v_1z=1 to get

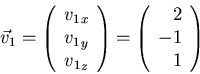
Eigenvectors corresponding to satisfy

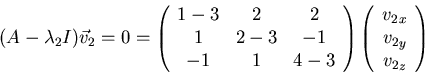
Solving using Gaussian elimination:

Equation (1') gives v_2x = v_2y + v_2z. There are two unknown parameters.

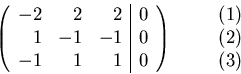
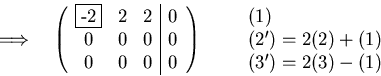
The general solution space is:

We need two independent eigenvectors to span the space corresponding to this multiple root.

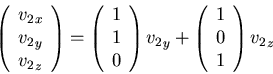
We can use the two vectors above, which means choosing v_2y=1 and v_2z=0 for one, and v_2y=0 and v_2z=1 for the other. That gives

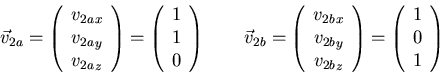
If the three vectors , , and are used as basis, A becomes diagonal. So despite the multiple root, this A is still diagonalizable. But if the solution space for the second eigenvalue would have been one-dimensional, the matrix would not have been diagonalizable.

10/09/02 0:12:08 10/09/02 0:32:39