Eigenvector Basis

Examples:

• decomposing motion along the fundamental modes;
• writing solid body motion along the principal axes;
• separation of variables;
• improving numerical schemes;
• ...

Diagonalization:

If we use the eigenvectors of a matrix A as basis, so that the transformation matrix P contains the eigenvectors:

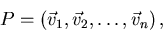
then the transformed matrix A' is diagonal:

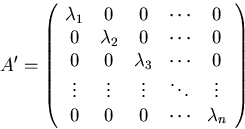
Reason: for any arbitrary vector

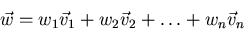
then

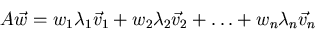
So A increases the first coefficient in the eigenvector basis by 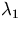, the second by 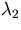, etcetera. That is exactly what the diagonal matrix A' does with the vector of coefficients .

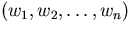Remember that the relationship between A and A' is

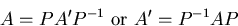
Note: If there are less than n independent eigenvectors, the matrix A is not diagonalizable. But as long as all n eigenvalues are unequal, there are always n independent eigenvectors.

10/07/02 0:30:02 10/09/02 0:05:25
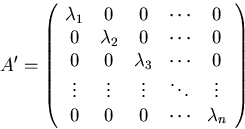