Introduction

Up: Contents

Introduction

Matrix operations:

Forming matrices;
Analyzing matrices;
Simplifying numerical solutions.

A matrix A is a table of numbers:

matrix consists of n column vectors (the columns), or equivalently of m row vectors (the rows).

Conversely, a column vector is equivalent to a matrix with only one column and a row vector is a matrix with only one row.

Index notation:

where

indicates ``the collection of values'' or ``set of values''.

Summation of two matrices (must be of the same size)

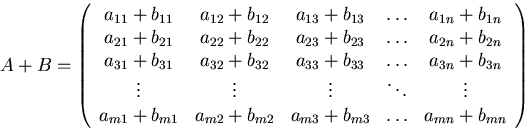
In other words, add corresponding components (just like for vectors)

Zero matrices have all coefficients zero. Adding a zero matrix to a matrix does not change the matrix.

Summation in index notation:

Scalar multiplication:

Just like for vectors.

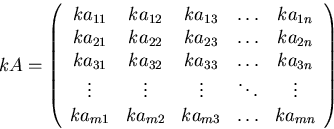
Scalar multiplication in index notation:

Transposing a matrix turns the columns into rows and vice-versa

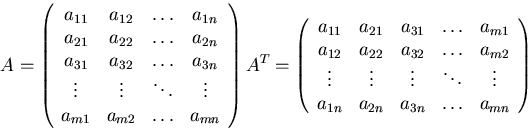
Similarly, transposing turns a column vector into a row vector and vice-versa.

Transpose in index notation:

Note that .

Matrix multiplication is defined in terms of the row-column product:

where

In other words, c_ij is the dot product of the i-th row-vector of A times the j-th column-vector of B:

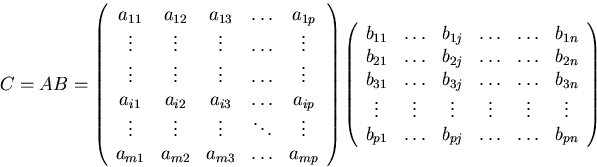
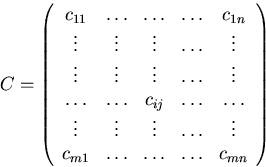
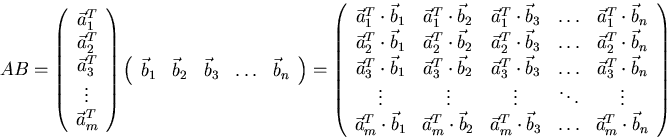
The dots in the above product can be omitted since the matrix product of a row vector times a column vector is by definition the same as the dot product of those vectors.

Multiplication in index notation:

The summation is over neighboring indices.

For matrices to be multiplied, the second dimension of A must be the same as the first dimension of B.

Matrix multiplication does not ordinarily commute:

Transposing matrix products:

(AB)^T = B^T A^T

Square matrices are matrices with the same number of rows as columns.

The main diagonal of a matrix A is the set of elements with i=j:

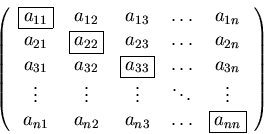
The trace of A is the sum of the diagonal elements:

Unit (or identity) matrix:

Note, blocks of zeros are often ommitted, (or written as a humongous zero,) so

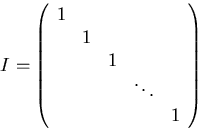
Index notation

The tensor

is called the Kronecker delta.

Multiplying a matrix by an identity matrix does not change the matrix.

Inverse matrices:

A A^-1 = A^-1 A = I

Note that

.The inverse only exists when the determinant of the matrix, |A|, is nonzero.

Inverting products:

(AB)^-1 = B^-1 A^-1

Inverting transposes:

Diagonal matrices:

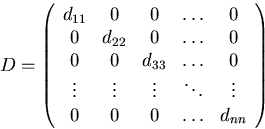
In index notation, d_ij=0 if .

Upper triangular matrices:

In index notation, u_ij=0 if j<i.

Lower triangular matrices:

In index notation, l_ij=0 if j>i.

Symmetric matrices satisfy S^T=S. Skew-symmetric matrices satisfy K^T= -K.

Orthonormal (orthogonal) matrices are matrices in which the columns vectors form an orthonormal set (each column vector has length one and is orthogonal to all the other colum vectors).

For square orthogonal matrices, the inverse is simply the transpose, O^-1 = O^T, as can be seen from:

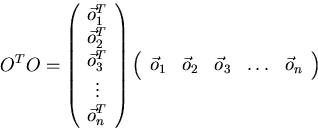
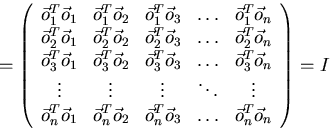
It can be seen, from inverting the order of the factors, that the rows of a square orthonormal matrices are an orthonormal set too.

``Normal'' matrices commute with their transpose: N^T N=N N^T. Symmetric, skew-symmetric, and orthonormal matrices are all normal.

For complex matrices, the generalization of transpose is ``Hermitian conjugate'', where you take the complex conjugate of each complex number, in addition to interchanging rows and columns: . Complex matrices for which A^H=A are called ``Hermitian matrices.'' Orthogonal matrices are now called ``unitary''. Normal matrices are still called ``normal.''

Up: Contents