Up: Contents
Introduction
Vectors:
- Statics and Dynamics
- Physics
- Geometry
- Computer solutions
- ...
Properties:
- Vectors as list of numbers:
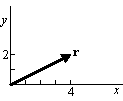
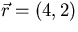 . If the list is written horizontally, the vector
is called a row vector; if it is written vertically, it is a column
vector. (To distinguish the rows and columns in matrices.)
. If the list is written horizontally, the vector
is called a row vector; if it is written vertically, it is a column
vector. (To distinguish the rows and columns in matrices.)
- Components: r1=x=4, r2=y=2.
- Base vectors:
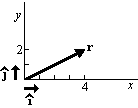
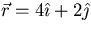 .
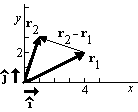
. - Addition:
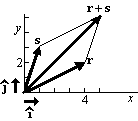
(4,2)+(1,3)=(4+1,2+3)=(5,5) or
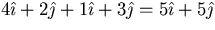 .
. - Multiplication by a scalar:
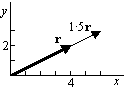
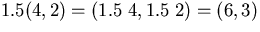 or
or
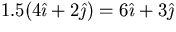 .
. - Dot (scalar) product:
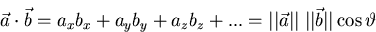
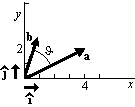
If the dot product is zero, the vectors are by definition orthogonal
to each other.
Length (norm) of a vector: 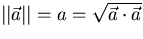 . Unit vectors have length one.
The distance between two points
. Unit vectors have length one.
The distance between two points 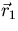 and
and 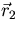 is by definition
is by definition
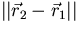 :
:
The projection of 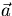 onto
onto 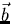 is
is
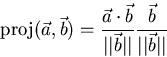
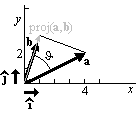
- Small determinants:
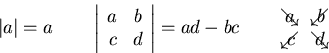
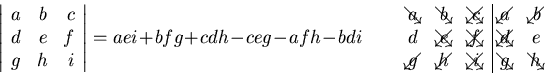
- Cross (vector) product in 3D:
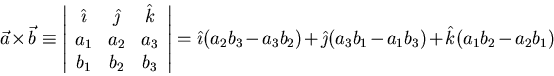
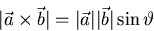
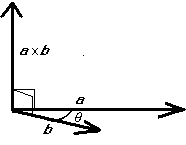
and normal to both vectors.
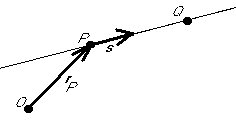
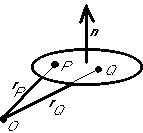
- Line through point P parallel to vector
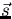 :
:
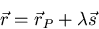
This applies to any number of dimensions.
- A hyperplane in Rn (n-dimensional space) is the points
satisfying a single scalar linear equation. In general:
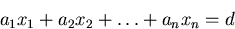
i.e.
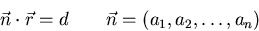
3D:
A plane:
a x + b y + c z = d
2D:
A line:
a x + b y = d
- Curves in Rn:
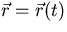 with t the parameter.
The unit tangent to the curve is
with t the parameter.
The unit tangent to the curve is 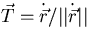 .
. - Tangent planes to a surface F(x,y,z)=0 at a point P on the surface:
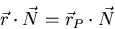
where N can be taken as the gradient 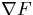 of F:
of F:
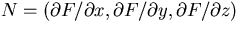
- Complex numbers:
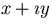 where
where 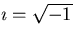 . Complex
numbers are special two-dimensional vectors. You get the complex
conjugate of a complex number by everywhere replacing
. Complex
numbers are special two-dimensional vectors. You get the complex
conjugate of a complex number by everywhere replacing 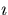 by
by
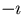 .
.
Up: Contents
 09/13/02 0:30:23
09/13/02 0:30:23
 09/16/02 0:25:26
09/16/02 0:25:26
 09/16/02 0:28:29
09/16/02 0:28:29
 09/18/02 0:10:56
09/18/02 0:10:56

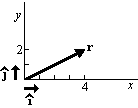


![]()
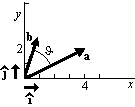

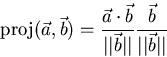

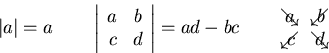
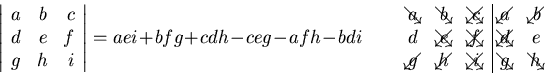
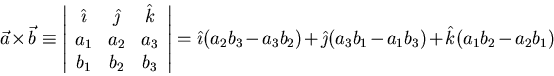
![]()


![]()
![]()
![]()

![]()

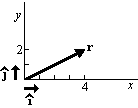


![]()
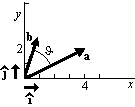

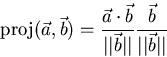

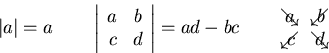
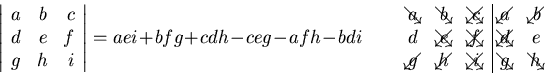
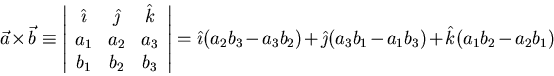
![]()


![]()
![]()
![]()

![]()