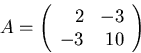
q = 2 x2 - 6 xy + 10 y2
Find the matrix of coefficients:
Eigenvalues:
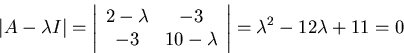
The eigenvector corresponding to ![]() satisfies
satisfies
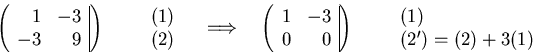
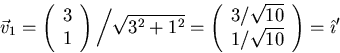
The eigenvector corresponding to ![]() satisfies
satisfies
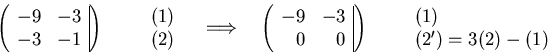
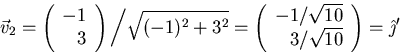
Since ![]() , the new axes are rotated
, the new axes are rotated
![]() counter clockwise from the old:
counter clockwise from the old:
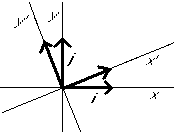
In the new coordinates,
![]()
Important note: It is seen that the quadratic form ![]() is always positive for nonzero
is always positive for nonzero ![]() . Symmetric matrices for
which this is true are called positive definite. They have all
positive eigenvalues. Similarly, if all eigenvalues are negative,
a symmetric matrix is called negative definite. If all eigenvalues
are positive or zero, it is called positive semi-definite.
. Symmetric matrices for
which this is true are called positive definite. They have all
positive eigenvalues. Similarly, if all eigenvalues are negative,
a symmetric matrix is called negative definite. If all eigenvalues
are positive or zero, it is called positive semi-definite.
Finite element codes for structures typically produce positive definite matrices, as do many other physical applications, such as the kinetic energy of a solid body. Definite matrices are typically easier to deal with in numerical applications than general matrices. For example, no pivoting is needed in the Gaussian elimination involving a definite matrix.