Up: Return
Introduction
Eigenvalues:
- buckling;
- modes of vibration;
- dynamical systems;
- principal axes;
- boundary layer instability;
- heat conduction;
- acoustics;
- electrical circuits;
- stability of numerical methods;
- exam questions;
- ...
Definition
A nonzero vector 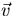 is an eigenvector of a matrix A if
is an eigenvector of a matrix A if 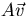 is
a multiple of
is
a multiple of 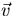 :
:
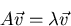
The number 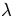 is called the corresponding eigenvalue.
is called the corresponding eigenvalue.
Graphically, if 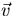 is an eigenvector of A, then the vector
is an eigenvector of A, then the vector
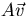 is in the same (or exactly opposite direction) as
is in the same (or exactly opposite direction) as 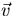 :
:
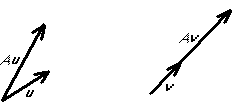
An eigenvector is indeterminate by a constant that must be chosen.
Example
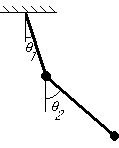
Equations of motion:
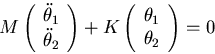
Setting 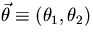
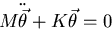
Premultiplying by M-1 and defining A=M-1K,
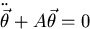
Try solutions of the form 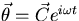 . The
constant vector
. The
constant vector 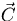 determines the ``mode shape:''
determines the ``mode shape:''
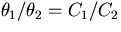 . The exponential gives the time-dependent
amplitude of this mode shape, with
. The exponential gives the time-dependent
amplitude of this mode shape, with 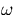 the natural frequency.
the natural frequency.
Plugging the assumed solution into the equations of motion:
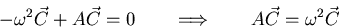
So the mode shape 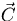 is an eigenvector of A and the
corresponding eigenvalue gives the square of the frequency.
is an eigenvector of A and the
corresponding eigenvalue gives the square of the frequency.
There will be two different eigenvectors 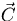 , hence two mode shapes
and two corresponding frequencies.
, hence two mode shapes
and two corresponding frequencies.
Note: we may lose symmetry in the above procedure. There are better
ways to do this.
Procedure
To find the eigenvalues and eigenvectors of a matrix A,
- 1.
- Find the zeros of the determinant
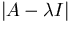 (i.e. of
matrix A with
(i.e. of
matrix A with 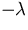 added to each main diagonal element.)
(The book uses
added to each main diagonal element.)
(The book uses 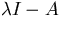 . This is very error-prone, and I do
not recommend it.) For an
. This is very error-prone, and I do
not recommend it.) For an 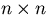 matrix A,
matrix A, 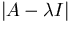 is an n-th degree polynomial in
is an n-th degree polynomial in 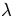 . From it, we can find
n eigenvalues
. From it, we can find
n eigenvalues 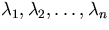 , (which do
not all need to be distinct, however.)
, (which do
not all need to be distinct, however.)
- 2.
- When the eigenvalues are found, for each eigenvalue
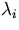 the corresponding eigenvector(s) can be found as the basis of the
null space of
the corresponding eigenvector(s) can be found as the basis of the
null space of 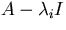 . Note: Do not leave
undetermined coefficients in eigenvectors. This is counted as an
error.
. Note: Do not leave
undetermined coefficients in eigenvectors. This is counted as an
error.
Up: Return
![]() is an eigenvector of a matrix A if
is an eigenvector of a matrix A if ![]() is
a multiple of
is
a multiple of ![]() :
:
![]()
![]() is an eigenvector of A, then the vector
is an eigenvector of A, then the vector
![]() is in the same (or exactly opposite direction) as
is in the same (or exactly opposite direction) as ![]() :
:
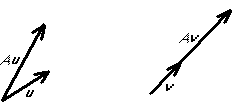

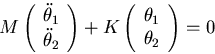
![]()
![]()
![]()
![]() . The
constant vector
. The
constant vector ![]() determines the ``mode shape:''
determines the ``mode shape:''
![]() . The exponential gives the time-dependent
amplitude of this mode shape, with
. The exponential gives the time-dependent
amplitude of this mode shape, with ![]() the natural frequency.
the natural frequency.
![]()
![]() , hence two mode shapes
and two corresponding frequencies.
, hence two mode shapes
and two corresponding frequencies.