Symmetric Matrices

Definition

A matrix A is symmetric if A^T=A.

Examples:

• mass and stiffness matrices found from the Lagrangian equations;
• finite element methods for structures, fluids, ...;
• inertia matrices of solid bodies;
• ...

Diagonalization:

• Symmetric matrices have real eigenvalues.
• Symmetric matrices always have a complete set of independent eigenvectors.
• These eigenvectors are (or at least can be taken to be) orthonormal.

For symmetric matrices, in this class you are required to orthonormalize the eigenvectors. As long as the null space of each eigenvalue has only one basis vector, this simply means normalizing the eigenvactor to length one (i.e. divide by its length.) If the null space has multiple basis vectors however, you will need to apply Gram-Schmidt on them or equivalent.

In either case, the result is that the eigenvectors to are an orthonormal set that we can indicate as ,and is no more than a rotated coordinate system. In other words, symmetric matrices are diagonalized by merely rotating the coordinate system.

As was mentioned in chapter 2, since the transformation matrix has orthonormal columns, it is called an orthonormal matrix. For any orthonormal matrix

P^-1 = P^T

Example:

Kinetic energy of a solid body:

where the x,y,z axis system has its origin at the center of gravity.

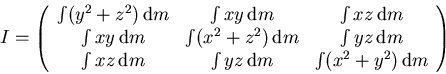
By rotating the x,y,z axis system to the principal axes of the body, the inertia matrix I becomes diagonal.

For a disk:

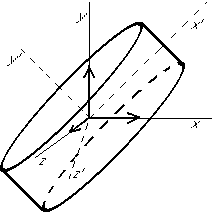
If you write the inertia matrix for a disk and find the eigenvalues, you will find one single eigenvalue and one double eigenvalue, giving the moments of inertia along the principal axes.

The eigenvector corresponding to the single eigenvalue will be in the y' direction; just normalize it to length one to give .

The eigenvector solution space corresponding to the double eigenvalue will have two independent basis vectors. Use Gram-Schmidt on them to orthonormalize them, that will poduce your and .

The axis system are the principal axes of the disk.