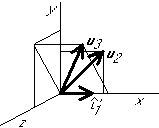Up: Return
Gram-Schmidt
Description:
Gram-Schmidt orthogonalization is a way of converting a given
arbitrary basis 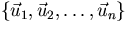 into an
equivalent orthonormal basis:
into an
equivalent orthonormal basis:
This often leads to better accuracy (e.g. in least square problems)
and/or simplifications.
Modified Gram-Schmidt Procedure
Given a set of linearly independent vectors,
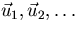 ,turn them into an equivalent orthonormal set
,turn them into an equivalent orthonormal set
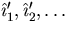 as follows:
as follows:
Step 1:
- 1.
- Normalize the first vector
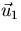 . That will be
your
. That will be
your 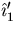
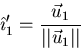
- 2.
- For the remaining vectors
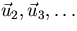 , eliminate their component in the direction of
, eliminate their component in the direction of 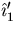 using the
following formula:
using the
following formula:
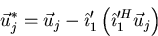
Note that 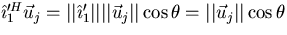 is the component of
is the component of 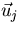 in the direction of
in the direction of 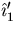 :
:
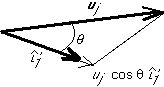
Also 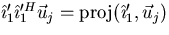 .The matrix
.The matrix 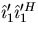 is called the projection operator
onto
is called the projection operator
onto 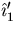 .
.
Ignore 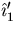 in the remaining process.
in the remaining process.
Step 2:
- 1.
- Normalize the second vector
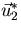 . That will be
your
. That will be
your 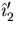
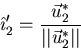
- 2.
- For the remaining vectors
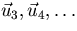 , eliminate their component in the direction of
, eliminate their component in the direction of 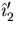 using the
following formula:
using the
following formula:
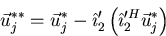
Ignore 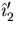 in the remaining process.
in the remaining process.
Repeat the process along the same lines until you run out of
vectors.
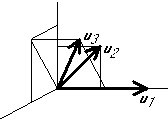
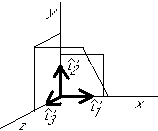
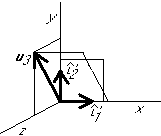
Graphical example:

Normalize 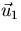 :
:
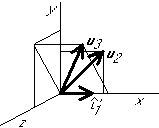
Eliminate the components in the 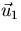 direction from the rest:
direction from the rest:
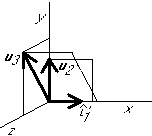
Normalize 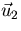 :
:
Eliminate the components in the 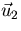 direction from the rest:
direction from the rest:
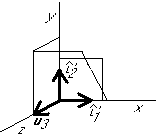
Normalize 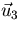 :
:

Up: Return
![]() into an
equivalent orthonormal basis:
into an
equivalent orthonormal basis:


![]() ,turn them into an equivalent orthonormal set
,turn them into an equivalent orthonormal set
![]() as follows:
as follows:
![]()
![]()
![]() is the component of
is the component of ![]() in the direction of
in the direction of ![]() :
:
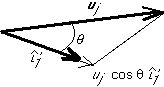
![]() in the remaining process.
in the remaining process.
![]()
![]()