4.89(a), §2 Solution

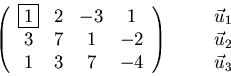
Most straightforward is to do Gaussian elimination with the vectors as rows:

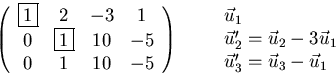
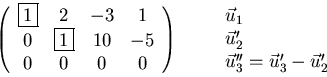
The vectors are linearly dependent, since the third vector is all zero. The rank of the matrix is 2: there are only two independent rows.

We can clean up a bit more by going to canonical:

The space spanned is then the set of linear combinations of the two simplified vectors. The first vector is normal to the y-axis, the second is normal to the x-axis.

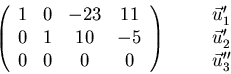
The alternate procedure uses the vectors as columns:

should have no nontrivial solutions for linear independence. Note that this produces the transpose matrix from the one above:

Since the solution of the system c₁, c₂, and c₃ can be nonzero, the vectors are linearly dependent.

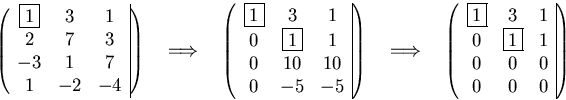
The number of independent rows in this matrix, which is the number of independent columns in the first matrix, is again 2. So the rank is 2 whether I look at rows or columns.

Why is the rank the same whether I take the vectors as rows or columns? Well, since there are two independent vectors (let's take them as the first two,) I can take c₃ whatever I want and only find unique values for c₁ and c₂ given c₃. That means there must be two nonzero pivots. So the number of independent row vectors established in the first method must be the number of pivots in the second method. And the number of pivots is the number of independent row vectors in the second matrix.