3.57(a), §2 Solution

We need c₁, c₂, and c₃ so that

In matrix form:

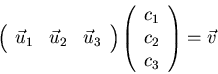
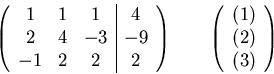
Forward elimination:

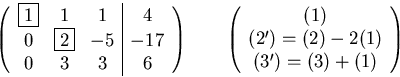
Back substitution:

From (3''), c₃=3; from (2'), c₂=-1; from (1), c₁=2.

If the right hand side would have been zero, the only possible values for c₁, c₂, and c₃ would be all zero. A set of vectors is dependent if you can create zero from them with some nonzero coefficients. (This allows you to express one of the set in terms of the others.)

Since you cannot do so with u₁, u₂ and u₃, they are independent vectors.

Also, since you can find a solution for any vector ,you can express any vector in terms of u₁, u₂, and u₃. Vectors for which that is true are called a basis, in this case for three-dimensional vector space.