Null spaces

The null space of a matrix A are all vectors so that . If A is square and |A| is nonzero, the null space is simply and has dimension 0.

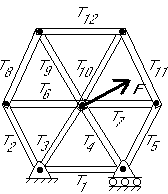
Nontrivial null spaces may correspond to internal stresses in structures, connectivity problems, vibrational mode shape, buckling shapes, eigenvectors corresponding to a given eigenvalue, etcetera.

You typically want to describe the null spaces as simply as possible. Defining a basis for the null space allows you to do so.