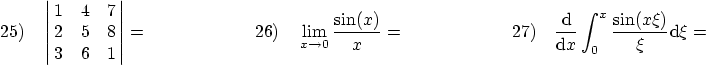|
|
|
Hand in the solution to this test on the date stated above (5% of your final grade). Read carefully. And look it up. Answer questions in the order listed. You must work alone. You probably want to consult your math handbook.
Neatly draw the graph of the following functions, showing the locations
of 0 and ![]() on each axis. Give the derivative. Indicate non-principal
values as a broken line. Make sure that you give enough of the curves
to clearly demonstrate all features.
Make sure that you have answered all parts, including derivatives.
on each axis. Give the derivative. Indicate non-principal
values as a broken line. Make sure that you give enough of the curves
to clearly demonstrate all features.
Make sure that you have answered all parts, including derivatives.
Find (include any integration constants and absolute signs):