- A company charges orders as follows
- Orders of 50,000 items or less are charged at $30 per
thousand.
- For orders above 50,000, the charge per thousand is reduced
by 37
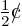 for each thousand above
50,000. (This reduced charge per thousand is applied to the
complete order.) for each thousand above
50,000. (This reduced charge per thousand is applied to the
complete order.)
Plot the receipts of this company versus order size and analyze
the graph for all features. What order size maximizes the
receipts of the company? Give the reasons why the financial
management of this company is clearly
incompetent.1. [1, Maximum and Minimum
Values]
- Inside a conical tent of height
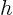 and radius of the base and radius of the base 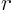 , a , a
living space is to be partioned in the shape of a
circular cylinder with a flat top of radius 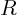 and height and height 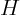 .
(a) Find the living space with the largest possible volume. (b)
Find the living space with the largest curved
surface.2. [1, Maximum and
Minimum Values] .
(a) Find the living space with the largest possible volume. (b)
Find the living space with the largest curved
surface.2. [1, Maximum and
Minimum Values]
- Find the MacLaurin series for
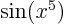 . Hint: you may not want
to crunch this out. Explain why not. Use a suitable trick
instead.
[1, Taylor and Maclaurin Series] . Hint: you may not want
to crunch this out. Explain why not. Use a suitable trick
instead.
[1, Taylor and Maclaurin Series]
- Write out the Taylor series for
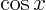 around around 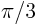 using the
exact values of using the
exact values of 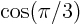 and and 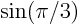 . Now assume that
you approximate the Taylor series by its first three terms. What
is the exact expression for the error in that approximation. How
can you approximate this error at values of . Now assume that
you approximate the Taylor series by its first three terms. What
is the exact expression for the error in that approximation. How
can you approximate this error at values of  close to close to 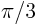 ?
Use the approximate error to find the distance ?
Use the approximate error to find the distance 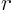 from from 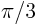 so
that the error is no more than 0.000 05 for all so
that the error is no more than 0.000 05 for all  for which for which
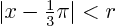 . Then improve on your error estimate to find a
more accurate value of . Then improve on your error estimate to find a
more accurate value of 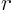 . [1, Taylor and Maclaurin
Series] . [1, Taylor and Maclaurin
Series]
- Find
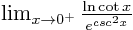 .
[1, L'Hôpital's Rule] .
[1, L'Hôpital's Rule]
- Find
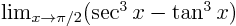 .
[1, L'Hôpital's Rule] .
[1, L'Hôpital's Rule]
- Variable
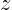 is given in terms of the measurable variables is given in terms of the measurable variables
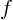 and and 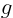 as as
The values of 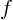 and and 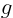 and their uncertainties are: and their uncertainties are:
What are the maximum relative and absolute errors in the computed
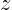 ? Are you stunned by the value of the relative error in ? Are you stunned by the value of the relative error in 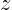 ?
Explain why not. [1, Total Differential] ?
Explain why not. [1, Total Differential]
|