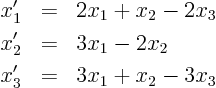|
|
|
|
Next: 12 Ordinary Differential Equations IV |
|
In this class,
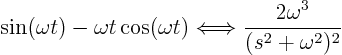
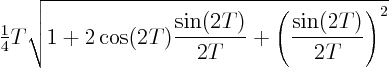
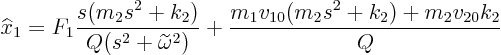
Now you need to find the qualitative form of the partial fraction
expansion of ![]() . Now the 4 roots of the quadratic
. Now the 4 roots of the quadratic ![]() in the bottom would be difficult to find.But look for a second at
the free solution (i.e. with
in the bottom would be difficult to find.But look for a second at
the free solution (i.e. with ![]() ). Based on your physical
arguments in the previous question, you should be able to describe
the qualitative nature of the four roots if the damping is low.
Knowing about the nature of these four roots, you can now ignore the
second term in
). Based on your physical
arguments in the previous question, you should be able to describe
the qualitative nature of the four roots if the damping is low.
Knowing about the nature of these four roots, you can now ignore the
second term in ![]() and look at the first term with
and look at the first term with ![]() nonzero. The terms will correspond to two decaying modes of
vibration and one term where
nonzero. The terms will correspond to two decaying modes of
vibration and one term where ![]() vibrates with frequency
vibrates with frequency
![]() . This term will have a large amplitude for small
damping. However, if you look a bit closer, you see that if you
choose the ratio
. This term will have a large amplitude for small
damping. However, if you look a bit closer, you see that if you
choose the ratio ![]() to be
to be ![]() , the third
term disappears. Then the building returns to rest after a
transition period, despite the ongoing vibrating force on it! The
effect of the force has been eliminated!
, the third
term disappears. Then the building returns to rest after a
transition period, despite the ongoing vibrating force on it! The
effect of the force has been eliminated!
You may be astonished by that, since only the ratio of ![]() to
to
![]() is specified. So you could eliminate the vibration in your
building
is specified. So you could eliminate the vibration in your
building ![]() by suspending a single grain of sand
by suspending a single grain of sand ![]() from it
using a very weak spring! (Actually, if you do this, and the
natural frequency of the building is close to
from it
using a very weak spring! (Actually, if you do this, and the
natural frequency of the building is close to ![]() ,
and damping is small, then the coefficients of the decaying modes
will be very large. So the building will still experience large
transient vibration.)
,
and damping is small, then the coefficients of the decaying modes
will be very large. So the building will still experience large
transient vibration.)