Find the volume of the region bounded by
Use cylindrical coordinates 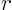 ,
, 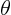 (or
(or 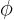 if you want),
and
if you want),
and 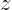 around the given
around the given 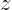 -axis.
-axis.
List the limits if (a) you do 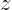 first, (b) you do r first, and (c)
you do
first, (b) you do r first, and (c)
you do 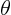 first. To do the latter two cases, make a picture
of the cross-section of the region for a fixed value of
first. To do the latter two cases, make a picture
of the cross-section of the region for a fixed value of 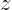 like
like
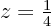 and show the
and show the 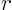 and
and 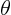 integration lines.
integration lines.
What variable is obviously the one to integrate first? For the
second integration, discuss each possibility and explain which is
the best choice. Use pictures to make your points.[1, Triple
Integrals]
![]() first, (b) you do r first, and (c)
you do
first, (b) you do r first, and (c)
you do ![]() first. To do the latter two cases, make a picture
of the cross-section of the region for a fixed value of
first. To do the latter two cases, make a picture
of the cross-section of the region for a fixed value of ![]() like
like
![]() and show the
and show the ![]() and
and ![]() integration lines.
integration lines.