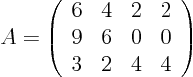|
|
|
|
Next: 7 Linear Algebra IV |
|
In this class,
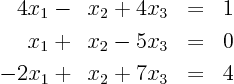
In the first stage of the forward elimination, you will first need
to do a partial pivoting to avoid fractions. In the second stage,
partial pivoting does no good, so should not be done. Since you
cannot take an integer multiple of the original equation different
from 1 in this question (since it would mess up the ![]() matrix asked
later) you will need to live with fractions in the final equation.
matrix asked
later) you will need to live with fractions in the final equation.
Solve the resulting equations using the class procedure.
Next do the same but using augmented matrix notation. (See also the revised notes on linear algebra.)
Next find the ![]() and
and ![]() matrices of the
matrices of the ![]() decomposition and
multiply the result. Do they give back the original matrix
decomposition and
multiply the result. Do they give back the original matrix ![]() of
the system. If not, what do they give back? So, what is the right
hand vector
of
the system. If not, what do they give back? So, what is the right
hand vector ![]() to use when solving
to use when solving ![]() ? Solve this system and check that you get indeed the correct
right hand side vector to use in solving the system
? Solve this system and check that you get indeed the correct
right hand side vector to use in solving the system ![]() . Double-check you are using the correct matrix and right hand
side while doing all the above. Make sure you have answered
everything. [2, 8.1].
. Double-check you are using the correct matrix and right hand
side while doing all the above. Make sure you have answered
everything. [2, 8.1].