- For a conical tent of given volume, find the ratio of the height
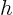 to the radius of the base to the radius of the base 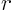 that requires the least amount
of material. Note: verify first that the surface area of a cone
is that requires the least amount
of material. Note: verify first that the surface area of a cone
is 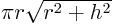 .1.
[1, Maximum and Minimum Values] .1.
[1, Maximum and Minimum Values]
- Inside a conical tent of height
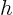 and radius of the base and radius of the base 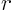 , a , a
living space is to be partioned in the shape of a
circular cylinder with a flat top of radius 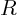 and height and height 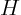 .
(a) Find the living space with the largest possible volume. (b)
Find the living space with the largest curved
surface.2. [1, Maximum and
Minimum Values] .
(a) Find the living space with the largest possible volume. (b)
Find the living space with the largest curved
surface.2. [1, Maximum and
Minimum Values]
- Find the MacLaurin series for
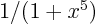 . Hint: you may not want
to crunch this out. Explain why not. Use a suitable trick
instead.
[1, Taylor and Maclaurin Series] . Hint: you may not want
to crunch this out. Explain why not. Use a suitable trick
instead.
[1, Taylor and Maclaurin Series]
- Write out the Taylor series for
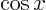 around around 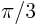 using the
exact values of using the
exact values of 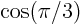 and and 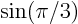 . Now assume that
you approximate the Taylor series by its first three terms. What
is the exact expression for the error in that approximation? How
can you approximate this error at values of . Now assume that
you approximate the Taylor series by its first three terms. What
is the exact expression for the error in that approximation? How
can you approximate this error at values of 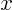 close to close to 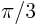 ?
Use the approximate error to find the distance ?
Use the approximate error to find the distance 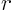 from from 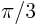 so
that the error is no more than 0.000 05 for all so
that the error is no more than 0.000 05 for all 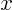 for which for which
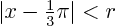 .
[1, Taylor and Maclaurin Series] .
[1, Taylor and Maclaurin Series]
- Find
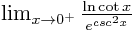 .
[1, L'Hôpital's Rule] .
[1, L'Hôpital's Rule]
- Find
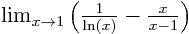 .
[1, L'Hôpital's Rule] .
[1, L'Hôpital's Rule]
|