8 Class Schedule

Class times: MWF 12:30-1:20 pm in A235 CEB (A building).

The below schedule is subject to change. Coverage shown is that of an earlier year, not necessarily this year.

08/26/19 M (Calc I) Syllabus. Graphs. Powers of .
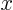08/28/19 W (Calc I) Graphs. Extents, intercepts, minima, maxima, horizontal, oblique, vertical asymptotes, slope and derivative, vertical slopes, corners, cusps, concavity, inflection points, second derivative.
08/30/19 F (Calc I) Due: Test 1. Example graphs.
09/02/19 M LABOR DAY
09/04/19 W (Calc II) Optimization. Constrained optimization.
09/06/19 F (Calc II) Due: HW Calc I. Lagrangian Multipliers. Approximation using Taylor series.
09/09/19 M (Calc II) Taylor series. Limits.
09/11/19 W (Calc III) Total differentials. Errors. Curvilinear motion.
09/13/19 F (Calc III) Due: HW Calc II. Multiple integrals.
09/16/19 M (Calc III) Multiple integrals. Numerical integration.
09/18/19 W (Lin I) Vectors. Lines. Planes. (from Calculus book). [Zill: 7.1-5]
09/20/19 F (Lin I) Due: HW Calc III. Vector spaces. Linear [in]dependence. Dimension. [Zill: 7.6]
09/23/19 M (Lin I) Matrices. Index notation. Matrix manipulations. Special Matrices. [Zill: 8.1].
09/25/19 W (Lin II) Calculus review? Start of Gaussian elimination. [Zill: 8.2].
09/27/19 F EXAM I Calculus
09/30/19 M (Lin II) Due: HW Lin I. Gaussian elimination. LU theorem. Operation counts. Band matrices. [Zill: 8.2?]
10/02/19 W (Lin II) Partial pivoting. Echelon form.
10/04/19 F (Lin III) General algorithm. Reduction to row-canonical form. Null space of a matrix.
10/07/19 M (Lin III) Due: HW Lin II. Solution space. Row space, column space, and rank of a matrix. Start of finding a simple row space basis.
10/09/19 W (Lin III) Finding simplified row and column space bases. Determinants. Co-factor (minor) expansion.
10/11/19 F (Lin IV) Determinants by Gaussian Elimination. Inverse matrices using minors and GE.
10/14/19 M (Lin IV) Due: HW Lin III. Eigenvectors and eigenvalues. Relation to nullspaces. Defective matrices.
10/16/19 W (Lin IV) Changes of coordinates. Diagonalization theorem. Matrix powers.
10/18/19 F (Lin V) Symmetric matrices. Rotation of the coordinate system.
10/21/19 M (Lin V) Due: HW Lin IV. Analysis of quadratic forms.
10/23/19 W (Lin V) Need for orthogonalization: Gram-Schmidt. Quadratic forms in 3D. Start of ODE.
10/25/19 F (ODE I) Intro. Direction fields. Separable equations. Linear equations.
10/28/19 M (ODE I) Due: HW Lin V. Homogeneous equation. Bernoulli equation.
10/30/19 W (ODE I) Lin review.
11/01/19 F EXAM II Linear Algebra
11/04/19 M (ODE II) Higher order equations. Homogeneous constant coefficient equations. Clean up of complex solutions. Inhomogeneous constant coefficient equations.
11/06/19 W (ODE II) Due: HW ODE I. Methods of undetermined coefficients and variation of parameters.
11/08/19 F (ODE II) Laplace transform solution. Partial fractions.
11/11/19 M VETERANS DAY
11/13/19 W (ODE III) General partial fractions. Shifting theorems. Heaviside step function.
11/15/19 F (ODE III) Due: HW ODE II. Dealing with singularities (jumps). Convolution theorem.
11/18/19 M (ODE III) Systems. Conversion to first order systems. Non-defective matrices. Clean up of complex eigenvalues.
11/20/19 W (ODE IV) Defective matrices.
11/22/19 F (ODE IV) Due: HW ODE III. Inhomogeneous CC systems. Initial conditions. Nonlinear systems. Autonomous systems.
11/25/19 M (ODE IV) Local linearization. Nature of the local solutions. Solution geometry and stability: real eigenvalues.
11/27/19 W THANKSGIVING
11/29/19 F THANKSGIVING
12/02/19 M (ODE V) Due: HW ODE IV. Solution geometry and stability: defective matrices and complex eigenvalues.
12/04/19 W (ODE V) Topology of solutions of nonlinear systems. Pendulum. Van der Pol oscillator: limit cycles.
12/06/19 F ODE review. Due: HW ODE V.
12/10/19 Tuesday 5:30-7:30 pm: FINAL EXAM ODE (in the usual classroom)
12/17/19 4:00 pm: Grades due online (Available next day)