12 Ordinary Differential Equations IV

In this class,

• Questions must be answered in order asked.
• Solutions must be neat.
• Solutions must be exact and fully simplified.
• You must use the given symbols.
• You must show all reasoning.
• Copying is never allowed, even when working together.

1. Given the system
   
   $$\dot {\vec x} = A \vec x \qquad A = \left(\begin{array}{cc} 0 & 5 -1 & -2 \end{array} \right)$$
   
   
   Find the general solution to this system in vector form and in terms of a fundamental matrix. Complex solutions not allowed.

2. Solve the system and initial condition
   
   $$\dot {\vec x} = A \vec x \quad \vec x(0) = \vec x_0 \qquad ... ...x_0 = \left( \begin{array}{c} 9 1 1 \end{array} \right)$$
   
   
   Give a fundamental matrix. Clean up the final $\vec x$.

3. Solve the inhomogeneous system and initial condition
   
   $$\dot {\vec x} = A \vec x + \vec g \quad \vec x(0) = \vec x... ...0 = \left( \begin{array}{c} 5 11 -2 \end{array} \right)$$
   
   
   Use variation of parameters. Clean up the final $\vec x$.

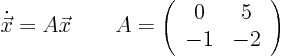
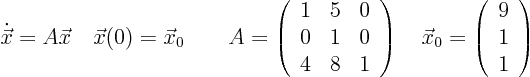
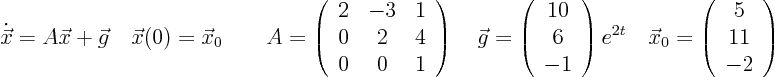
4. UNGRADED BUT NEEDED LATER ANYWAY: Consider the autonomous system
   

   $$x' = x + 3y - x^2 \sin y \qquad y' = 2x + y - x y^2$$
   
   

   Analyze this system analytically:

   1. Find the critical points. One critical point is easy. Four more critical points can be found numerically (like using fzero in MATLAB). To help you a bit, their $y$-values are $\pm1.1107$ and $\pm1.6074$.
   2. Find the matrix of derivatives of vector $\vec F$ at each of the five critical point. (By symmetry around the origin, there are only three matrices that are different.)

5. UNGRADED BUT NEEDED LATER ANYWAY: For each of the three different matrices of the previous question, solve the linearized system. (For the simple point, your solution should be exact. For the other points, check your calculations.) State the type of stationary point and its stability. For each point, draw the linearized solution lines near the stationary point accurately.

   Hints, for the simple point, one eigenvalue is $1{+}\sqrt{6}$. For the other two, one eigenvalue is $-7.12$, respectively 2.61. Make sure you get the directions of the eigenvectors right in all three cases.

   Next draw the phase plane, with $-3\le x\le 3$ and $-2\le y\le 2$ and locate the five stationary points. At each stationary point, draw a miniature version of the corresponding graph above. It should be small enough not to get anywhere close to the other stationary point pictures. In the next homework you will be asked to tie the solution lines of these pictures together.