- For a conical tent of given volume, find the ratio of the height
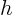 to the radius of the base to the radius of the base 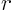 that requires the least amount
of material. Note: prove first that the surface area of a cone
(without base) is that requires the least amount
of material. Note: prove first that the surface area of a cone
(without base) is 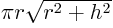 .
1.
[1, Maximum and Minimum Values] .
1.
[1, Maximum and Minimum Values]
- Inside a conical tent of height
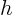 and radius of the base and radius of the base 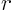 , a , a
living space is to be partioned in the shape of a
circular cylinder with a flat top of radius 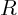 and height and height 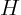 .
(a) Find the living space with the largest possible volume. (b)
Find the living space with the largest curved
surface.2. [1, Maximum and
Minimum Values] .
(a) Find the living space with the largest possible volume. (b)
Find the living space with the largest curved
surface.2. [1, Maximum and
Minimum Values]
|