| Page | HW | Class | Topic: |
| 110 (126) | 15 (29) | 16 (30) | optimization |
| 111 (128) | 25 (43) | - | optimization |
| 171 (369) | 11 (11) | 14 (14) | velocity and acceleration |
| 171 (369) | 15 (15) | - | velocity and acceleration |
| 181 (000) | 42 (00) | - | velocity and acceleration |
| 195 (249) | 26 (10e) | 43 (10v) | limits |
| 195 (250) | 51 (10d') | 47 (10z) | limits |
| 205 (139) | 26 (00) | 28 (00) | curve tracing |
| 205 (139) | 38 (00) | 33 (00) | curve tracing |
| 290 (520) | 19 (00) | 18 (00) | centroid of an area |
| 291 (541) | 38 (00) | 35 (00) | of a solid of revolution |
| 300 (000) | 12 (00) | 9a (00) | fluid pressure |
| 304 (000) | 19 (00) | - | work |
| 365 (430) | 21 (00) | 20 (00) | numerical approximation |
| 374 (440) | 17 (29) | 18 (30) | numerical approximation |
| 379 (223) | 10 (00) | 12 (00) | numerical integration |
| 392 (461) | 25b (27b) | 25a (27a) | absolute, relative errors |
| 392 (461) | 28 (30) | 27 (29) | time-rate of changes |
| 410 (477) | 35 (35) | 35b (35b) | lines and planes |
| 410 (477) | 36 (36) | 36b (36b) | area in space |
| 434 (510) | 24 (24) | 24a (24a) | work, conservative forces |
| 434 (510) | 26 (26) | - | derivatives of potentials |
| 447 (528) | 13f (13f) | - | area |
| 447 (528) | 14e (14e) | - | centroid |
| 447 (528) | 16b (16b) | - | moments of inertia |
| 450 (537) | 17 (22) | 19 (24) | volume |
| 464 (549) | 20a (20a) | - | volume |
| 464 (549) | 21a (21a) | - | centroid |
| 464 (550) | 22a (22a) | 22c (22c) | moments of inertia |
The question and page numbers within the parentheses are for the 4th edition of the book. The questions I cannot find in my 4th edition follow:
Page 181, 42: A particle moves counter-clockwise on ![]() with a constant speed of 4 units/sec. Express
with a constant speed of 4 units/sec. Express ![]() and
and ![]() in terms of
in terms of ![]() and
and ![]() .Note:
.Note: ![]() and
and
![]() .(Answer:
.(Answer:
![]() ;
;![]() .)
.)
Page 205, 26: Discuss and sketch (x2-16)y2 = x3 (x-2).
Page 205, 38: Discuss and sketch y=x2/3-x5/3.
Page 290, 19: Find the centroid of the area between 3y2 = 4(3-x), x=0. (Answer: 6/5,0.)
Page 291, 38: Find the centroid of the body of revolution obtained by
rotating the first quadrant area bounded by y2 = 12 x and its latus
rectum about the directrix.
(Answer: ![]() .)
.)
Page 300, 12: A cylindrical tank 6 ft in radius is lying on its side.
If it contains oil weighing w lb/ft3 to a depth of 9 ft, find the
force on an end.
(Answer ![]() lb.)
lb.)
Page 304, 16: Show that the work done in pumping out a tank is equal to the work that would be done by lifting the contents from the center of gravity of the liquid to the outlet.
Page 306, 19: Air is confined in a cylinder fitted with a piston. At a pressure of 20 lb/ft2, the volume is 100 ft3. Find the work done on the piston when the air is compressed to 2 ft3 (a) assuming pv= constant; (b) assuming pv1.4= constant. (Answer: (a) 7824 ft-lb; (b) 18,910 ft-lb.)
Page 365, 21: Show that
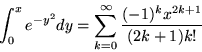
Page 379, 10: Approximate ![]() using
(a) the trapezoidal rule with n= 5 and (b) the Simpson rule
with n=4.
(Answer: (a) 1.115; (b) 1.111)
using
(a) the trapezoidal rule with n= 5 and (b) the Simpson rule
with n=4.
(Answer: (a) 1.115; (b) 1.111)
Page 434, 24: In each of the following, find the work done by the given force
![]() in moving a particle from (0,0,0) to (1,1,1) along (1) the
straight line x=y=z, (2) the curve x=t, y=t2, z=t3, and
(3) the straight lines from (0,0,0) to (1,0,0), (1,0,0) to (1,1,0),
(1.1,0) to (1,1,1).
(a)
in moving a particle from (0,0,0) to (1,1,1) along (1) the
straight line x=y=z, (2) the curve x=t, y=t2, z=t3, and
(3) the straight lines from (0,0,0) to (1,0,0), (1,0,0) to (1,1,0),
(1.1,0) to (1,1,1).
(a) ![]() (b)
(b) ![]() (c)
(c) ![]() (Answer: (a) 3; (b) 3; (c) 9/4, 33/14, 5/2.)
(Answer: (a) 3; (b) 3; (c) 9/4, 33/14, 5/2.)
Page 434, 26: Show that (a) ![]() ;and (b)
;and (b) ![]() .
.
Page 447, 13f: Use double integration to find the area outside
![]() and inside
and inside ![]() . (Answer:
. (Answer: ![]() .)
.)
Page 447, 14e: Use double integration to find the centroid of the first quadrant area bounded by x2 -8y +4=0, x2=4y, x=0. (Answer: 3/4, 2/5.)
Page 447, 16b: Use double integration to find Ix and Iy for
the area cut from y2=8x by its latus rectum.
(Answer: ![]() ,
, ![]() .)
.)